不确定的类型（不确定极限）

在这篇文章中，我们解释什么是不确定性。您将发现所有类型的不确定性是什么以及如何解决它们。此外，您将能够看到逐步解决所有不确定性函数极限的练习。

什么是不确定性？

不定式，也称为不定形式，是出现在结果未定义的函数极限计算中的数学表达式。因此，为了解决极限的不确定性，有必要应用取决于函数类型的初步程序。

也就是说，当我们得到不确定性时，并不意味着极限不存在或无法求解，而是意味着我们必须对函数进行更改才能找到极限的解。

不确定性的类型

不确定或不确定形式分为以下类型：

• 不确定性 无穷大减无穷大(无穷大-无穷大)
• 零之间的不确定数(k/∞)
• 零之间的零不确定性(0/0)
• 无穷大 (无穷大/无穷大) 之间的无限不确定性
• 不确定性 1 提高到无穷大(1 ^∞ )
• 零不确定性提升至零(0 ⁰ )
• 无穷大的零不确定性(0·∞)
• 零不确定性提升至无穷大(0 ^∞ )
• 无限不确定性为零(∞ ⁰ )

然后我们将看到如何解决所有类型的不确定性。

无穷负无穷不确定性

不定形式无穷大减无穷大不等于零，因为我们减去两个非常大的数，但我们不知道哪个更大。因此，无穷大之差的结果取决于每个无穷大的阶数。

解决这种类型的不确定性并不容易，因为根据函数的类型，必须应用一种或另一种过程。因此，我们建议您在以下链接中查看完整的说明：

➤请参阅： 如何解决不确定性无穷大减去无穷大

零之间的不确定数

当有理函数的分母被取消时，得到常数除以零的不确定性。

这种不定形式的结果总是更大、更小或者函数的极限不存在。让我们以求解极限为例来看看如何计算这种不确定性：

我们已经得到了一个数除以零的不确定性，因此我们需要计算函数的横向极限：

➤请参阅：什么是横向限制？

函数的两个横向极限给出相同的结果，因此根据定义，当 x 趋于 0 时函数的极限给出负无穷大：

请注意，如果横向极限给出了不同的值，则此时函数的极限将不存在。

零之间的不确定性

不确定极限零除以零是很常见的，并且是在分子和分母抵消的分数函数中获得的。

根据函数的不同，这种类型的不确定极限的解决方式也不同。例如，如果函数有根，则必须执行不同的步骤。您可以在以下链接中查看此类不确定性的不同解决方案：

➤参见： 如何解决零之间的零不确定性

无限之间的无限不确定性

无穷大之间的无限不确定性通常出现在带有分数的函数的无穷极限中。尽管不确定性是两个无穷大的商，但结果不一定是无穷大。

这种不确定形式是通过比较来解决的。即，观察分子的次数和分母的次数，根据哪一个较大，极限结果是其中之一或另一个。您可以在以下链接中查看所有案例：

➤请参阅：已解决的关于无穷大之间的无限极限的练习

不确定性 1 提高到无穷大

从数学上讲，人们可能会认为1 到无穷大等于 1，因为 1 的任何幂都等于 1。然而，这项是不确定性的，因此，人们不能轻易地推导出它的结果。

这种类型的不确定性通过应用以下公式计算：

例如，以下极限是不确定的，因为它给出了无穷大的幂：

因此，我们必须使用此类不确定性的公式：

因此我们已经解决了将不确定极限提高到无穷大的问题。

零不确定性归零

零幂的零不确定性出现在复杂函数的极限内。

要解决这种类型的不确定限制，您必须使用以下限制属性：

例如，以下极限给出了不定形式 0 的 0 次方：

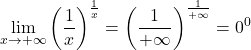
但如果我们对极限取对数，我们可以找到它的值：

无穷大的零不确定性

零和无穷大的乘积的不确定性很难遇到，但这并不意味着它很容易确定。

没有单一的方法可以解决这种类型的不确定性，但它取决于函数的类型。在这种情况下，我们必须将函数转换为无限不确定性除以无穷大或零不确定性除以零，并从那里应用我们上面看到的每个不确定性的求解方法。

因此，如果一个函数的极限为 0，另一个函数的极限为 ∞：

我们可以通过进行以下更改来无限地转换此类型：

让我们以解决不确定极限为例来看看如何做到这一点：

我们对函数进行运算以获得无穷大的无限不确定性，然后找到极限：

零不确定性提高到无穷大

将不确定性零提升到无穷大有点难以理解，因为我们正在将一个非常小的数字提升到一个非常大的数字。

当获得这些不定形式时，必须使用以下公式：

让我们解决一个例子，以更好地理解如何计算这种类型的不确定性：

无限不确定性归零

通常，任何幂为零时都会得到 1，但是，无穷大的不确定性为零时不一定是这样。

正如在不确定性中，零升到零和零升到无穷大，要解决这种类型的不确定极限，有必要应用对数：

让我们通过逐步计算示例来看看如何解决此类不确定极限：