一次方程或线性方程是代数的基础,因为如果你不理解它们,你将很难理解更复杂的方程。因此,此类方程的特殊性在于单项式的文字部分不能有指数。因此,在线性方程中,我们只会找到没有文字部分的单项式和有文字部分但没有指数的单项式,例如: 3 + x = -5 – 3x 。
另请注意,这些方程通常有唯一解,但也可能没有。为了知道我们面临的是哪种情况,我们必须求解方程并最终分析结果。因此,如果我们得到一个不可能的等式,例如 2 = 0,则方程无解。另一方面,如果我们得到一个始终为真的等式,那么解就等价于所有实数。最后,如果最后我们获得 X 和一个数值相等,在这种情况下我们将得到一个唯一的结果。
求解线性方程的过程
求解方程相当于计算变量的值,用字母 (x, y, a, b…) 表示。因此,要找到这个值,我们需要执行以下步骤:
- 求解括号和分数:首先,我们删除所有括号和分母,以获得更容易理解的方程。因为我们可以直接了解哪些术语伴随着未知数,哪些不伴随着未知数,所以这种阅读使我们能够轻松地继续解析表达式。
- 让我们简化表达式:我们将相似的项分组(一方面是独立的项,另一方面是带有 x 的项)。因此,在一侧,我们将留下未知数的数字,并将其他数字传递到另一侧。但请记住,要改变他们的立场,我们必须改变他们的标志。
- 每边运算:我们按以下顺序执行所有运算:幂/根、乘法/除法和加法/减法。我们这样做,直到每边都有一个项,因此我们最终得到一个与此结构相同的方程:4x = 8。
- 隔离变量:最后,只需通过在另一侧除法来传递字母附带的值,即可找到其最终值。在此步骤结束时,我们将解决未知问题,并且我们将知道剩下什么类型的结果:唯一的解决方案、无效的解决方案或满足所有整数的解决方案。
一次方程的例子
下面您将找到已解的一次方程,它们根据其结构的复杂性分为不同的类别。因此,了解了求解线性方程的理论过程和存在的不同类型,您就已经具备了能够轻松求解它们的必要知识,我们将从实践开始。也就是说,让我们从理论解释开始:
基本一次方程
第一种类型的线性方程仅包含基本算术运算(加法、减法、乘法和除法)。这里有两个例子,第一个是更基本的,第二个是在计算方面更复杂的:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
带括号的一次方程
其次,我们在括号中列出线性方程。这些问题比前面的问题解决起来稍微复杂一些,尽管它们唯一的困难在于计算,因为必须尊重括号的属性。为了更清楚地说明这一点,我们向您展示两个有效的示例:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
具有幂和根的一次方程
第三层就很简单了,只是增加了力量和根源。使用这些方程时您可能遇到的唯一困难是当指数或根影响整数括号时(就像我们将向您展示的第二个示例),但其他所有内容几乎保持不变。下面是两个例子。
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
带分数的一次方程
我们可以找到的最后一类线性方程是这个方程,它由我们之前评论过的所有元素以及分数组成。这一级是最复杂的,有多种方法可以解决。第一个也是最简单的方法是将分母乘以等式的另一边,尽管我们只能在有两个分数时使用它。另一方面,如果方程中有两个以上的分数,我们必须找到一个公分母,并将所有分数相乘,将该值除以同一分数的分母。下面是每种类型的示例:
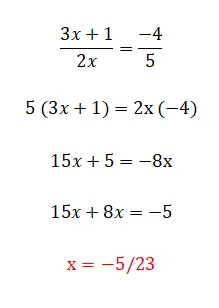
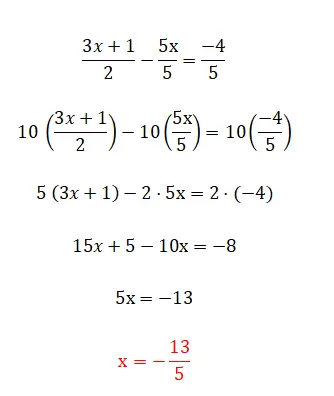
一次方程练习
现在我们提供一些线性方程练习。它们按照难度的增加进行组织,第一个方程比最后一个方程更容易。因此,我们建议您从头开始,看看您能走多远。因此,请尝试求解以下方程,然后将您的结果与我们提供的解决方案进行比较。
第一个练习
第一个练习是一个非常简单的线性方程,因为它只包含加法和减法,并且等式两边之间也只有四项:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- 我们将相似的术语组合在一起。
- 我们简化双方。
- 我们删除未知数并计算它的值。
第二个练习
在这种情况下,我们发现自己有一个由括号组成的方程,我们的首要任务是消除它们,以便我们可以将相似的项分组在一起:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- 我们解决括号。
- 我们将 x 移至左侧,将独立项移至右侧。
- 我们澄清未知的事情。
我们简化结果。
第三个练习
接下来,您需要求解另一个带括号的二次方程,尽管这个方程有点困难。这是因为它有嵌套括号(括号内有其他括号)。因此,必须正确遵循解决的顺序:先内部人,后外部人。
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- 我们首先解决内括号。
- 接下来,我们解析外括号。
- 我们简化等式两边并收集相似的术语。
- 我们分离 x 并计算它的值。
第四个练习
在本练习中,我们开始看到分数,它可能是线性方程中最复杂的元素。不过不用担心,因为如果您阅读了理论,您就会完全知道如何做到这一点:
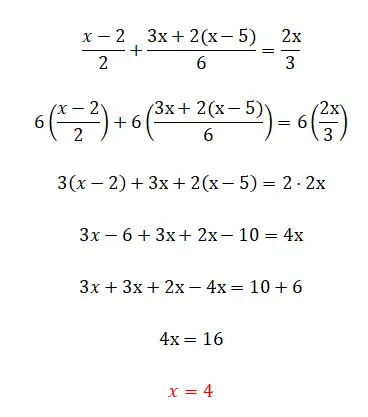
第五练习
在第五个练习中,我们看到括号中的分数,这意味着求解层次结构变得有点复杂。值得一提的是,这个例子可以用两种方法来求解:使用最小公倍数法或直接用分数运算。下面你可以看到两个完整的过程:
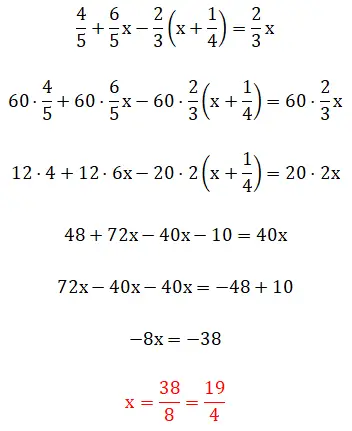
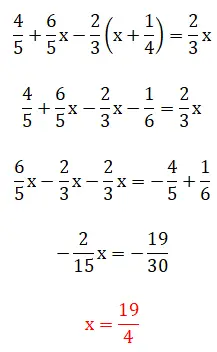
第六个练习
接下来,我们进一步讨论分数和括号的主题,因为我们有嵌套的括号。与上一个练习相比,这个练习并没有带来更多的复杂性,只是在计算方面稍微困难一些,仅此而已。
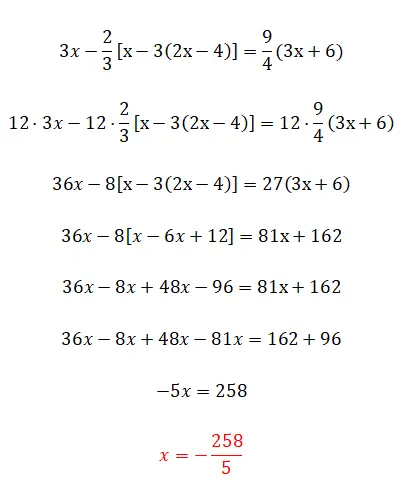
- 我们将所有项乘以分母的 lcmp。
- 我们通过删除括号来简化表达式:首先是里面的括号,然后是外面的括号。
- 我们将每一侧相似的术语分组。
- 我们解决双方的操作。
- 我们计算未知数的值。
第七个练习
下面的练习可能看起来很简单,但我们建议您无论如何都尝试解决它,因为它肯定会给您带来一些不寻常的结果。尝试完后看练习下面的解决方案和解释。
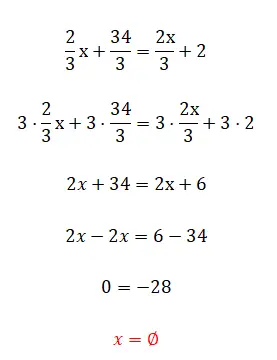
- 我们将所有分数与分母的 lcm 相乘。
- 我们简化得到的表达式。
- 最后我们看到它给了我们一个错误的平等,因为我们已经消除了未知数。
您可能已经注意到,这是错误的等式或没有结果的等式,因为没有值可以正确完成方程。这是我们在引言中提到的案例之一。
第八个练习
最后,我们为您提供这个相当复杂的练习,因为它具有我们在本文中看到的所有复杂性,尽管它也有一个小技巧。评论说,如果你能够解出这个一级方程,那么你就已经完全理解了整个理论。如果没有,请不要担心,因为这个练习非常复杂。
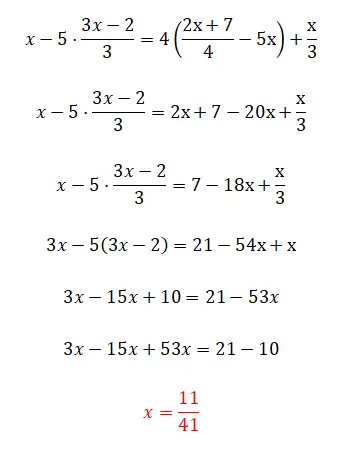
- 我们首先消除等式右侧的四个。
- 然后我们将右侧的 x 连接起来。
- 我们将所有项乘以三,以消除分母。
- 我们删除括号。
- 我们将类似的术语放在一起。
- 我们计算未知数的值。
更多线性方程练习
现在您已经有了足够的练习,您应该能够求解复杂的线性方程。不过,如果您想继续练习,我们建议您尝试解决此工作表。但如果您认为您已经了解得足够多,我们还可以为您提供一篇文章来帮助您了解操作的层次结构。这样您就可以始终知道首先要解决哪个计算,并且永远不会出错。