空间中两条线之间的距离（以 r3 为单位）

在此页面上，您将了解如何计算空间中两条线之间的距离（在 R3 中），无论其类型如何（平行线、割线、重合线、割线、垂直线等）。此外，您将能够看到逐步解决的示例和练习。

如何计算两条线之间的距离

两条线之间的距离是一条线上任意点与另一条线上任意点之间的最小距离。该距离对应于从一条线到另一条线并且同时垂直于两条线的线段的长度。

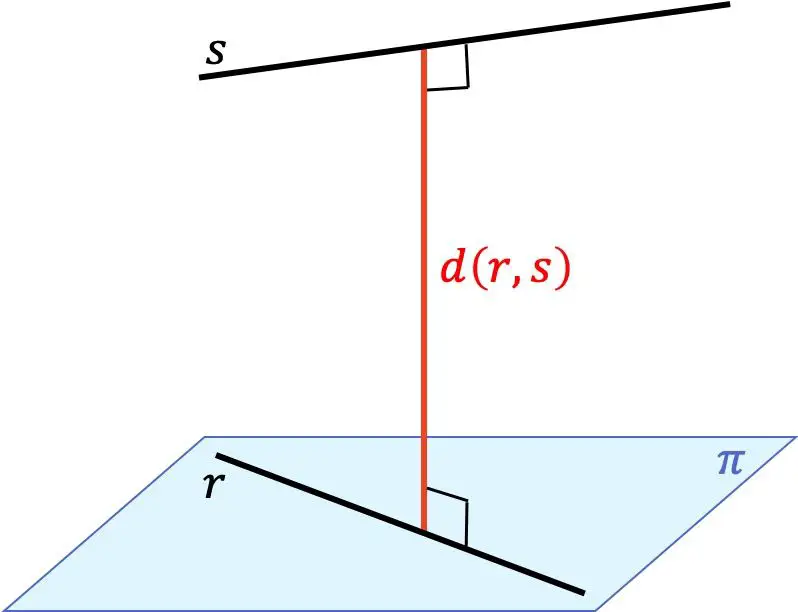
因此，在三维 (3D) 空间中查找两条不同线之间的距离取决于它们之间的相对位置：

• 如果两条线重合或相交，则两条线之间的距离为零，因为它们（至少）相交于一点。
• 当两条线平行时，我们需要取其中一条线上的任意点并计算该点与另一条线之间的距离（下面有一个示例说明如何执行此操作）。
• 如果两条线在空间中相交，我们需要应用两条相交线之间的距离公式（详细解释见下文）。

因此，要计算两条线之间的距离，您必须首先知道它们是什么类型的线，然后根据情况使用一种或另一种公式。因此，在继续之前，您已经掌握了如何找到两条线在空间中的相对位置，这一点很重要，但如果您不记得链接中是如何完成的，您将看到非常完整的解释以及已解决的示例和练习一步步。

如何求空间中两条平行线之间的距离

计算空间中两条平行线之间的距离（在 R3 中）与在平面中（在 R2 中）相同：您必须在两条线上的任何一条线上取一点，并找到该点在另一条线上的距离线。

举个例子，我们要解决空间中两条平行线之间的距离问题：

• 下面两条平行线之间的距离是多少？

两条直线都以向量方程的形式表示，因此，我们可以很容易地找出它们各自的方向向量和点：

如果您对如何确定直线的方向向量和点有任何疑问，我们建议您看一下直线方程的解释。在那里，我们对直线的所有方程进行了解释，因为找到方向向量和属于直线的点取决于表达直线的方程类型。

现在，要找到两条平行线之间的距离，我们需要应用点到线的距离公式：

因此，一方面我们计算向量乘积产生的向量的模。如果您对它的计算方式有疑问，可以查阅向量乘积公式，此外，您还可以在其中看到向量之间这种运算的示例和已解决的练习。

另一方面，我们找到直线向量的大小

最后，我们将每一项的值代入公式并计算线之间的距离：

因此，两条线之间的距离为 3.60 个单位。

如何确定空间中两条相交线之间的距离

正如我们在开始时看到的，确定两条相交线之间的距离的方法与确定平行线之间的距离的过程不同。

因此，有多种方法可以确定空间中两条相交线之间的距离。本页我们只讲解一个过程，最简单的，因为另外两种方法较长且较复杂，实际上并没有用到。

为了让您了解如何确定两条交叉线之间的距离，我们将解决一个问题作为示例：

• 接下来两条相交线之间的距离是多少？

首先，我们需要识别方向向量和每条线上的点。两条直线以连续方程的形式表示，因此：

现在我们应用两条相交线之间距离的公式：

一方面，我们求解混合积（或三重标量积）：

另一方面，我们找到叉积（或叉积）的模：

最后，我们将公式中每一项的值替换为两条交叉线之间的距离：