克莱默法则 - Mathority

在此页面上，您将了解什么是克莱默规则，此外，您还将找到通过克莱默规则求解方程组的示例和练习。

什么是克莱默法则？

克莱默法则是一种用于通过行列式求解方程组的方法。我们来看看它是如何使用的：

考虑一个方程组：

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

系统的矩阵A和扩展矩阵A’为：

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

克莱默法则指出方程组的解为：

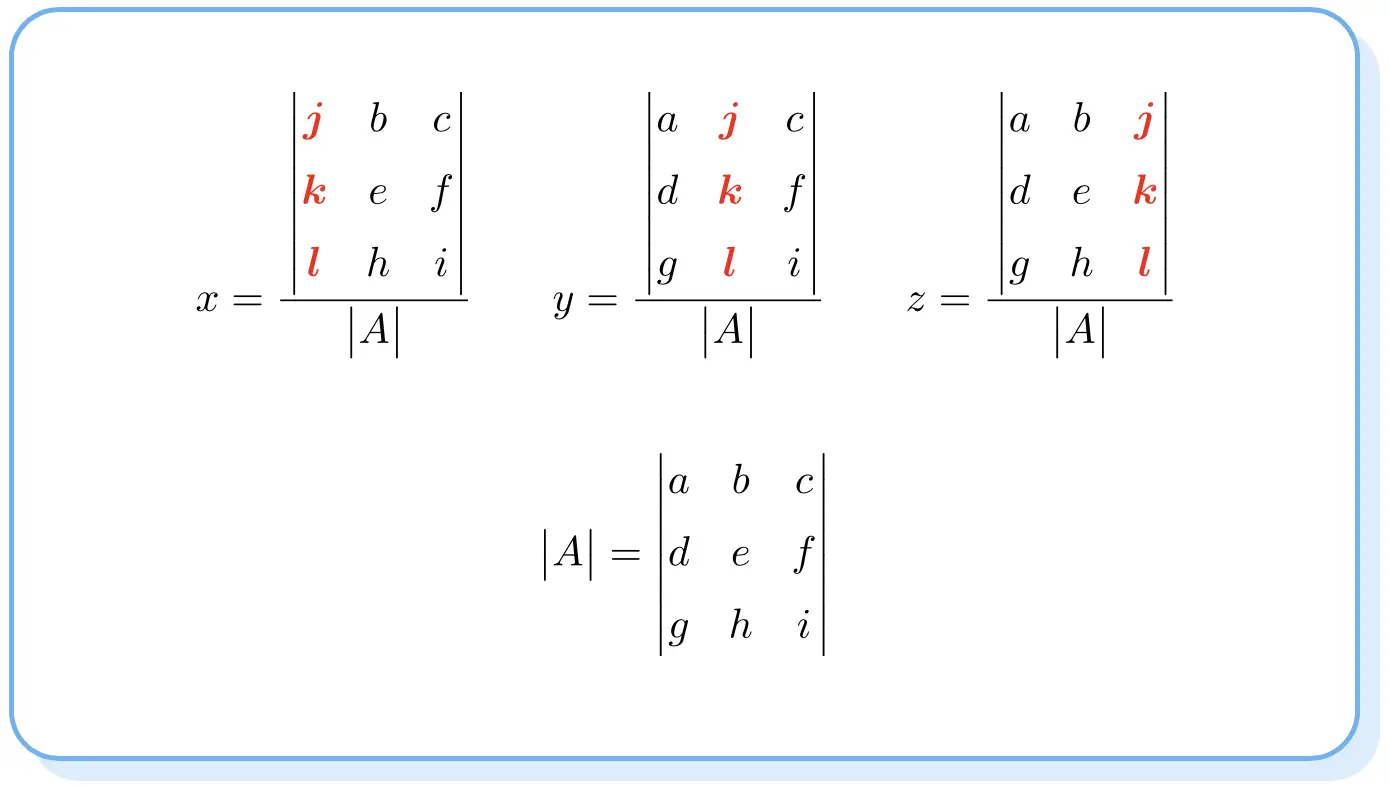
请注意，分子的行列式类似于矩阵 A 的行列式，但将每个未知数的列更改为独立项的列。

因此，克莱默法则用于求解线性方程组。但是，正如您所知，求解方程组的方法有很多，例如众所周知的高斯乔丹方法。

以下是使用克莱默法则（有时也写为克莱默法则）求解线性方程组的示例。

示例1：确定兼容系统（SCD）

使用克莱默法则求解以下具有 3 个未知数的 3 个方程组：

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

现在我们计算两个矩阵的秩，以了解它是什么类型的系统。为了计算 A 的秩，我们计算整个矩阵的 3×3 行列式（使用 Sarrus 规则）并查看它是否给出 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

A 的行列式不为 0，因此矩阵 A 的秩为 3。

$\displaystyle rg(A)=3$

因此，矩阵 A’ 的秩也是 3 ，因为它不能是秩 4 并且必须至少与矩阵 A 具有相同的秩。

$\displaystyle rg(A')=3$

矩阵 A 的范围等于矩阵 A’ 的范围和系统 (3) 的未知数个数，因此，根据Rouché-Frobenius 定理，我们知道它是一个确定的兼容系统（SCD）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

一旦我们知道系统是一个 SCD，我们就应用克莱默规则来解决它。为此，请回想一下矩阵 A、其行列式和矩阵 A’ 为：

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

计算

$\displaystyle z$

根据克莱默规则，我们将 A 行列式的第三列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

因此，方程组的解为：

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

示例 2：不确定兼容系统 (ICS)

使用克莱默法则求解以下方程组：

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

现在我们计算两个矩阵的范围，从而可以看出它是什么类型的系统。为了计算 A 的秩，我们计算整个矩阵的行列式（使用 Sarrus 规则）并检查它是否为 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

行列式给出 0，因此矩阵 A 的秩不是 3。但它有一个不同于 0 的 2×2 行列式：

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

所以矩阵 A 的秩为 2 ：

$\displaystyle rg(A)=2$

一旦我们知道了矩阵 A 的范围，我们就可以计算矩阵 A’ 的范围。前 3 列的行列式给出 0，因此我们尝试矩阵 A’ 中其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

所有 3 阶行列式都给出 0。但是，显然，矩阵 A’ 具有与矩阵 A 相同的非 0 2×2 行列式：

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

因此，矩阵 A’ 的秩也是 2 ：

$\displaystyle rg(A')=2$

因此，由于矩阵 A 的秩等于矩阵 A’ 的秩，但这两个值均小于系统 (3) 的未知数个数，因此根据Rouché-Frobenius 定理可知，这是一个不定相容系统（工业控制系统）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

当我们想要求解相容不定系统（SCI）时，我们需要对系统进行变换：首先消去一个方程，然后将一个变量转换为 λ（通常是变量 z），最后将 λ 项与独立条款。

一旦我们改造了系统，我们应用克拉默规则，我们将获得系统作为 λ 函数的解。

在这种情况下，我们将从系统中消除最后一个方程：

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

现在让我们将变量 z 转换为 λ：

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

我们将带有 λ 的项与独立项放在一起：

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

因此，系统的矩阵A和矩阵A’仍为：

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

最后，一旦我们改变了系统，我们就应用克莱默规则。因此我们求解 A 的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

虽然方程组的解是 λ 的函数，但由于它是 SCI，因此它有无穷多个解：

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

克莱默法则解决了问题

练习1

应用克莱默法则求解以下具有 2 个未知数的两个方程组：

查看解决方案

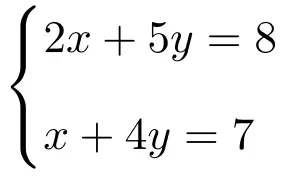
首先要做的是系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

我们现在必须找到矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

由于矩阵具有不同于 0 的 2×2 行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。这至少是 2 阶的，因为我们刚刚看到它内部有一个不同于 0 的 2 阶行列式。此外，它不可能是 3 阶的，因为我们不能不做一个 3×3 行列式。因此，矩阵 A’ 的秩也是 2：

$\displaystyle rg(A')=2$

因此，通过应用Rouché-Frobenius定理，我们知道这是一个兼容的确定系统（SCD），因为A的范围等于A’的范围和未知数的数量。

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

一旦我们知道系统是一个 SCD，我们就应用克莱默规则来解决它。

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

因此，方程组的解为：

$\displaystyle \bm{x = -1 \qquad y=2}$

练习2

使用克莱默法则求以下具有 3 个未知数的三个方程组的解：

查看解决方案

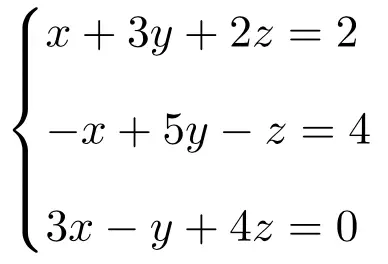
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

现在，我们通过使用 Sarrus 规则计算 3×3 矩阵的行列式来找到矩阵 A 的秩：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

具有不同于 0 的 3 阶行列式的矩阵，矩阵 A 的秩为 3：

$\displaystyle rg(A)=3$

因此，矩阵 A’ 的秩也是 3：

$\displaystyle rg(A')=3$

因此，利用Rouché-Frobenius 定理，我们知道这是一个兼容的确定系统（SCD），因为 A 的范围等于 A’ 的范围和未知数的数量。

一旦我们知道该系统是一个SCD，我们就需要应用克莱默规则来求解该系统。

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

计算

$\displaystyle z$

根据克莱默规则，我们将 A 行列式的第三列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

因此，方程组的解为：

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

练习3

使用克莱默法则计算以下具有 3 个未知数的三个方程组的解：

查看解决方案

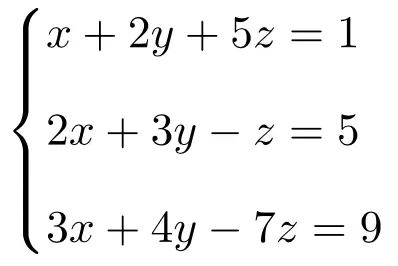
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

我们计算矩阵 A 的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

一旦我们知道了矩阵 A 的范围，我们就可以计算矩阵 A’ 的范围。前 3 列的行列式给出 0，因此我们尝试矩阵 A’ 中其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

所有 3 阶行列式都给出 0。然而，矩阵 A’ 具有与矩阵 A 相同的 2×2 非 0 行列式：

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

因此，矩阵 A’ 的秩也是 2：

$\displaystyle rg(A')=2$

由于矩阵 A 的秩等于矩阵 A’ 的秩，但这两者都小于系统 (3) 的未知数个数，因此根据Rouché-Frobenius 定理可知它是一个不定相容系统(ICS)：

作为 ICS 系统，我们必须消除一个方程。在这种情况下，我们将从系统中消除最后一个方程：

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

现在让我们将变量 z 转换为 λ：

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

我们将带有 λ 的项与独立项放在一起：

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

使得系统的矩阵A和矩阵A’保持：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

最后，一旦我们改变了系统，我们就应用克莱默规则。因此我们求解 A 的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

虽然方程组的解是 λ 的函数，但由于它是 SCI，因此它有无穷多个解：

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

练习4

应用克莱默规则求解以下具有 3 个未知数的三方程组问题：

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

查看解决方案

首先构造系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

现在让我们通过使用 Sarrus 规则计算 3×3 矩阵的行列式来计算矩阵 A 的秩：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

具有不同于 0 的 3 阶行列式的矩阵，矩阵 A 的秩为 3：

$\displaystyle rg(A)=3$

因此，矩阵 A’ 的秩也是 3，因为它必须至少与矩阵 A 具有相同的秩，并且它不能是秩 4，因为它是维度为 3×4 的矩阵。

$\displaystyle rg(A')=3$

因此，利用Rouché-Frobenius 定理，我们推断它是一个确定兼容系统（SCD），因为 A 的范围等于 A’ 的范围和未知数的数量。

一旦我们知道该系统是一个SCD，我们就需要应用克莱默规则来求解该系统。

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

计算

$\displaystyle z$

根据克莱默规则，我们将 A 行列式的第三列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

因此，线性方程组的解为：

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

练习5

使用克莱默法则求解以下线性方程组：

查看解决方案

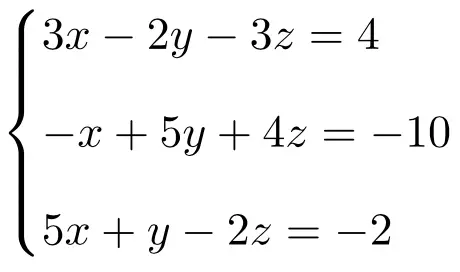
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

我们计算矩阵 A 的范围：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

一旦我们知道了矩阵 A 的范围，我们就可以计算矩阵 A’ 的范围。前 3 列的行列式给出 0，因此我们尝试矩阵 A’ 中其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

所有 3 阶行列式都给出 0。但是，显然，矩阵 A’ 与矩阵 A 具有相同的 2 阶行列式（除了 0）：

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

因此，矩阵 A’ 的秩也是 2：

$\displaystyle rg(A')=2$

矩阵 A 的秩等于矩阵 A’ 的秩，但这两个都小于系统的未知数数 (3)，因此根据Rouché-Frobenius 定理我们知道它是一个不定系统兼容(SCI) :

作为一个 ICS 系统，我们必须消除一个方程。在这种情况下，我们将从系统中消除最后一个方程：

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

现在让我们将变量 z 转换为 λ：

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

我们将带有 λ 的项与独立项放在一起：

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

使得系统的矩阵A和矩阵A’保持：

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

最后，一旦我们改变了系统，我们就应用克莱默规则。因此我们求解 A 的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

计算未知数

$\displaystyle x$

根据克莱默规则，我们将 A 行列式的第一列更改为独立项列，然后将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

计算未知数

$\displaystyle y$

根据克莱默规则，我们将 A 行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

因此，方程组的解是 λ 的函数，因为它是一个 SCI，因此该方程组有无穷多个解：

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

什么是克莱默法则？

示例1：确定兼容系统（SCD）

示例 2：不确定兼容系统 (ICS)

克莱默法则解决了问题

练习1

练习2

练习3

练习4

练习5

发表评论 取消回复

发表评论取消回复