在本文中,我们将解释如何导出函数的双曲反余切值。此外,您将能够看到双曲反余切导数的求解示例。
双曲反余切导数的公式
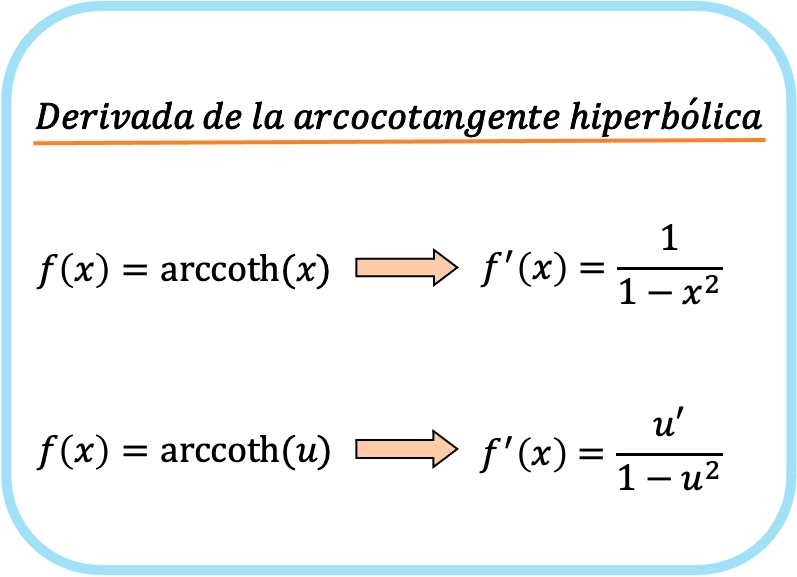
x 的双曲反余切值的导数等于一减 x 平方。
![]()
因此,函数双曲反余切的导数等于该函数的导数除以一减去该函数的平方所得的商。
![]()
请注意,第二个公式与第一个公式类似,但应用了链式法则,因此它们实际上可以被视为相同的公式。
你可能在一些数学书上看到,这类反三角函数的导数是:
![]()
但仔细一看,它们是同一个公式,唯一的区别是分数的分子和分母都乘以-1。
双曲反余切导数的示例
实施例1
![]()
在双曲反余切参数中,我们有一个与 x 不同的函数,因此我们需要使用链式法则公式来推导它:
![]()
5x 的导数是 5,因此将 5 放入分数的分子中,并将负 5x 的平方放入分母中:
![]()
实施例2
![]()
为了求解该函数的导数,我们需要应用双曲反余切的导数公式,如下所示:
![]()
在这种情况下,我们有一个复合函数,因为三角函数的参数中有一个指数函数。所以我们需要利用链式法则求整个函数的导数:
![]()