在本文中,我们将解释如何导出函数的双曲正割。您将找到双曲正割导数的公式以及此类导数的几个工作示例。
双曲正割的导数公式
x 的双曲正割的导数等于减去 x 的双曲正割乘以 x 的双曲正切的乘积。
![]()
因此,函数的双曲正割的导数减去函数的双曲正割乘以函数的双曲正切乘以所述函数的导数的乘积。
![]()
简而言之,双曲正割函数的导数公式为:
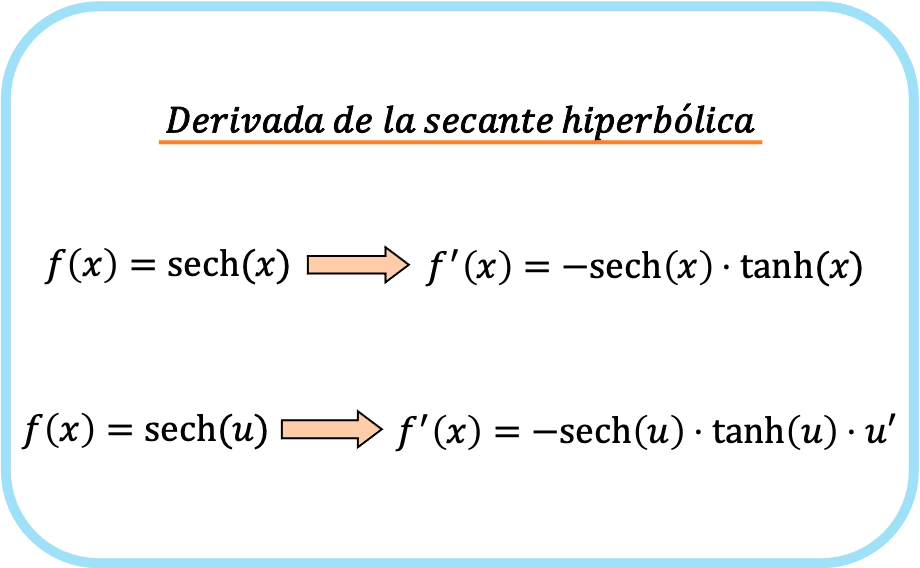
请注意,两个表达式实际上属于一个公式。唯一的区别是在第二个公式中应用了链式法则。
双曲正割的导数示例
现在我们知道了双曲正割导数的公式,我们将看到此类三角导数的几个已解决的练习。
实施例1
![]()
在此示例中,我们在双曲正割参数中具有与 x 不同的函数,因此要导出它,我们需要使用链式法则公式。
![]()
由于函数 2x 是线性的,因此它的导数为 2。因此,要求导数,我们只需将公式中的 u 替换为 2x,将 u’ 替换为 2:
![]()
实施例2
![]()
这个练习的功能是复合的,因为双曲正割在其论证中还有另一个功能。因此我们必须使用双曲正割公式和链式法则来进行推导:
![]()
x 的导数升到 2 得到 2x,因此 x 平方的双曲正割的导数为:
![]()