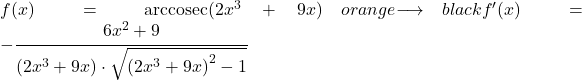在此页面上,您将看到反余割导数的公式是什么。此外,您将能够看到函数反余割导数的已解决练习。
反余割导数公式
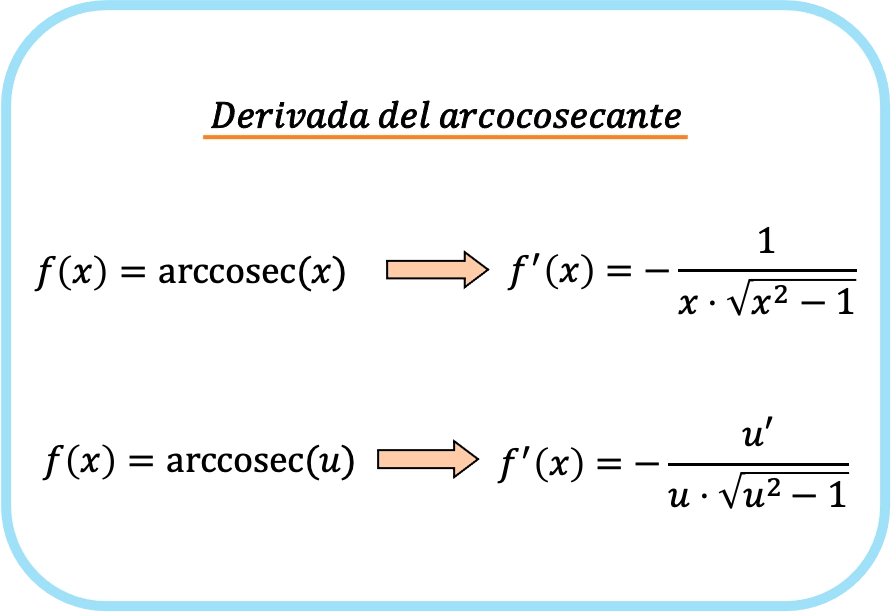
x 的反余割的导数为 x 乘以 x 平方根减 1 的乘积的负一。
![]()
因此,函数的反余割的导数等于减去该函数的导数除以该函数的商乘以该函数的平方减一的根。
![]()
事实上,前两个公式是相同的,但在第二个表达式中应用了链式法则。事实上,如果将恒等函数 x 代入 u,就会得到 x 的反余割的导数,因为 x 的导数是 1。
众所周知,反余割是余割的反三角函数,但其导数却截然不同。您可以在以下链接中查看这种其他类型的三角函数的公式:
➤请参阅:余割的导数
余割弧的导数示例
了解了反余割导数规则是什么,接下来我们将求解此类导数的两个示例。但如果您对如何推导余割弧还有任何疑问,可以在评论中询问我们。
实施例1
在这个例子中,我们将看到二次函数 x 2的反余割的导数是多少。
![]()
为了计算 x 平方的反余割的导数,我们应用上面看到的公式:
![]()
x 的 2 次方导数为 2x,因此复合函数的导数为:
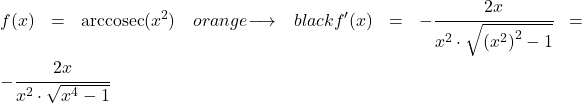
实施例2
在第二个示例中,我们将导出势函数的反余割。
![]()
我们需要使用反正割导数规则来求整个函数的导数。
![]()
因此,在分子中我们写下函数自变量的导数,在分母中我们重写势函数并将其乘以自变量函数平方减 1 的平方根: