在此页面上,您将看到双曲反余弦的导数(公式)。您还可以找到逐步解决函数双曲反余弦导数的练习。最后,您将找到此类三角函数的导数公式的演示。
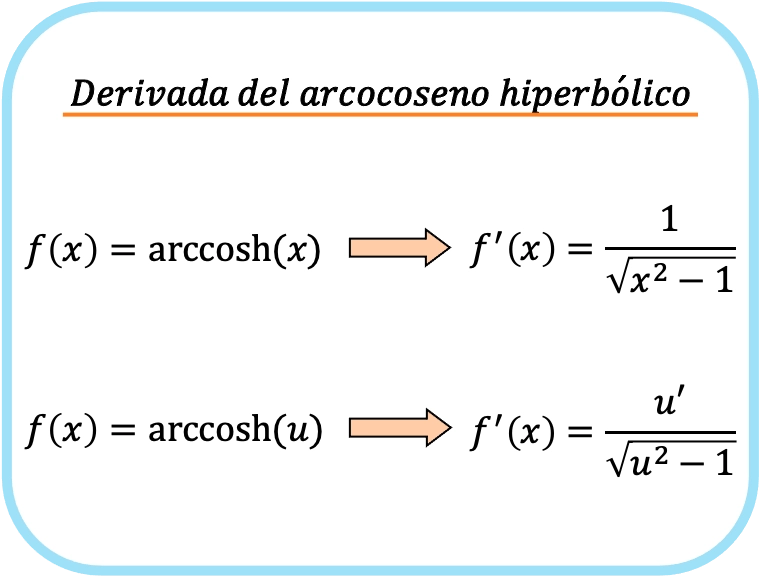
双曲反余弦导数公式
x 的双曲反余弦的导数是 x 平方减 1 的平方根除以 1。
![]()
因此,函数的双曲反余弦导数等于该函数的导数除以该函数的平方减一的平方根的商。
![]()
第二个公式包括链式法则,因此可用于导出任何双曲反余弦。事实上,如果我们用 u 代替 x,我们就会得到第一个公式。相反,第一个公式仅适用于 x 的双曲反余弦导数。
双曲反余弦是双曲余弦的反函数,因此这两个函数是相关的。您可以点击此处查看该三角函数的导数公式:
➤参见:双曲余弦导数公式
双曲反正弦导数的示例
实施例1
![]()
为了求双曲反余弦的导数,我们需要使用其相应的公式,即:
![]()
因此,在分数的分子中,我们需要输入 5x 的导数,即 5。在分母中,我们只需输入参数函数的平方减 1 的平方根:
![]()
实施例2
![]()
本练习要导出的函数是双曲反余弦,因此我们使用以下公式来导出它:
![]()
因此,在分子中我们写下函数自变量的导数,在分母中写出自变量函数的平方根加到 2 减 1:
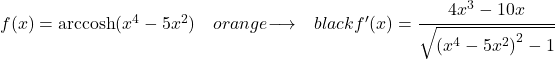
双曲反余弦导数的证明
最后,我们将演示双曲反余弦导数的公式。
![]()
首先,我们将双曲反余弦转换为双曲余弦:
![]()
我们从等式两边推导出:
![]()
我们清除你:
![]()
我们现在使用将双曲正弦和双曲余弦联系起来的三角恒等式来修改分母:
![]()
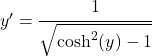
然而,首先,我们推导出 x 等于 y 的双曲余弦,因此方程仍然成立:
![]()