在本文中,我们将解释如何导出函数的反正弦。您会找到函数反正弦导数的示例,甚至可以通过逐步解决的练习进行练习。最后,您还将看到反正弦导数公式的演示。
反正弦的导数是什么?
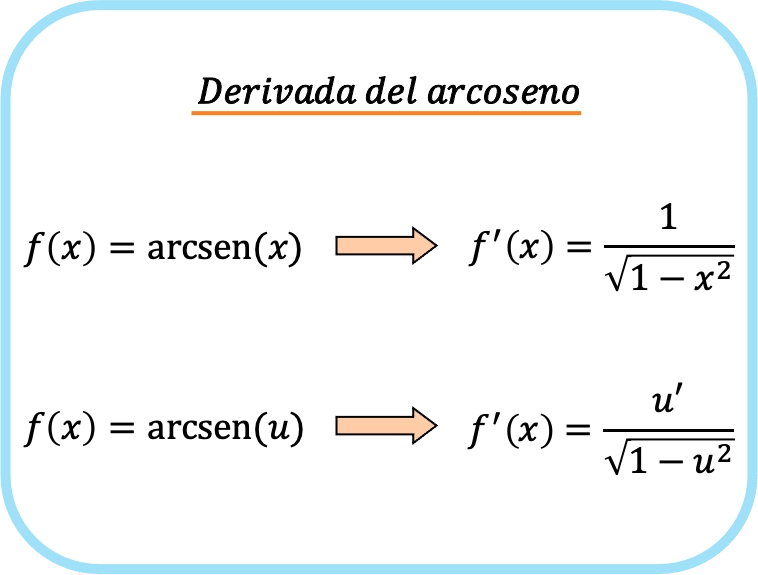
x 的反正弦导数是 1 减去 x 平方的平方根除以 1。
![]()
因此,函数反正弦的导数等于该函数的导数除以一的平方根减去函数平方所得的商。
![]()
从逻辑上讲,第二个公式是通过对第一个公式应用链式法则得到的。
请记住,反正弦是正弦的反函数,这就是为什么它也称为反正弦。
反正弦导数的示例
了解反正弦导数的公式是什么后,我们将解释此类三角导数的几个示例。这样你会更容易理解函数的反正弦是如何导出的。
示例 1:2x 反正弦的导数
![]()
要求反正弦函数的导数,我们需要使用其相应的公式:
![]()
因此 2x 的导数为 2,因此 2x 的反正弦导数为 2 除以 1 的根减去 2x 的平方:
![]()
示例 2:x 平方反正弦的导数
![]()
我们用反正弦导数公式来推导:
![]()
函数 x 2是二阶函数,因此其导数为 2x。因此,x 的反正弦的 2 次方的导数为:
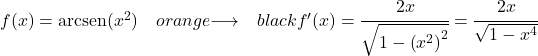
示例 3: ex的反正弦导数
![]()
本例中的函数是复合函数,因此我们需要应用链式法则来求解导数:
![]()
e x的导数是它本身,所以整个函数的导数是:
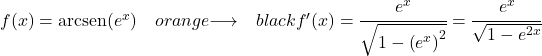
反正弦导数已解决的问题
推导以下反正弦函数:
![]()
![]()
![]()
![]()
![]()
查看解决方案
![]()
![]()
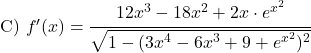
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
反正弦导数公式的证明
接下来,我们继续对反正弦导数公式进行数学证明。
![]()
首先,我们将反正弦转换为正弦:
![]()
现在我们对方程两边求导:
![]()
我们清除你:
![]()
接下来,我们应用基本三角恒等式:
![]()
![]()
并且,正如我们上面推导出的,x 等于 y 的正弦,等式仍然成立:
![]()
正如你所看到的,通过应用这个过程,我们得到了反正弦函数的导数公式,因此表明该公式是满足的。