在这里,我们解释如何求根(或根式函数)的导数。您将找到根除法的公式以及根的导数的逐步求解练习。
根的导数公式
根或无理函数的导数等于被被数(根式下面的表达式)的导数除以根的指数乘以同根的乘积,再从被被数的指数中减去 1。
![]()
但是,如果根被数只是 x,则公式会简化。因此 x 的根导数如下:
![]()
简而言之,求根的公式有两个:第一个总是可以使用,第二个只有当被数为 x 时才可以使用。
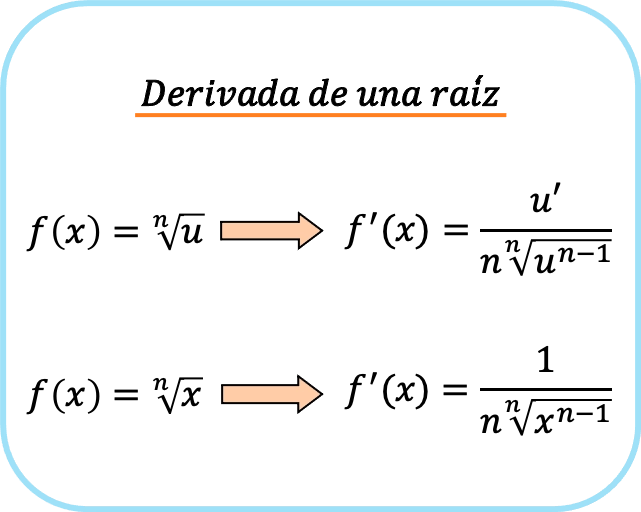
如果仔细观察,分数分子中的项是在求根的导数时应用链式法则得到的结果。这就是为什么当被数为 x 时,1 出现在分母中,因为它是 x 的导数。
根导数的例子
给定根函数的导数公式,下面我们将解释此类导数的几个示例,以便您了解如何求根的导数。
示例 1:平方根的导数
然后我们将看到平方根的导数是什么:
![]()
在这种情况下,根内部的表达式只是一个 x,因此我们可以使用以下公式:
![]()
因此,平方根的导数等于 1 除以 2 乘以 x 的平方根的乘积:
![]()
示例 2:立方根的导数
![]()
在这个例子中,根下的表达式是x,所以我们可以应用以下公式:
![]()
因此,立方根的导数等于 1 除以 3 乘以 x 平方根的立方根:
![]()
示例 3:四次方根的导数
![]()
现在我们的根号下面没有x,但是我们确实有一个更复杂的代数表达式。因此,我们必须使用根导数的一般公式:
![]()
根式下的表达式是一次函数,因此它的导数为7。因此,整个函数的导数为:
![]()
示例 4:从一个根到另一个根的推导
![]()
为了求解这个根由另一个根组成的导数,我们必须应用以下公式:
![]()
在这种情况下,您必须连续两次使用相同的公式来计算导数:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37131b50bda38022296c6401af727ce_l3.png)
解决了根的导数问题
计算以下根的导数:
![]()
![]()
![]()
![]()
![]()
![]()
查看解决方案
![]()
![Rendered by QuickLaTeX.com \text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bacf51d3e3fd8fa192f982456f2a8d6_l3.png)
![]()
![Rendered by QuickLaTeX.com \text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5169c93bdfa2522a3219563eee1bb354_l3.png)
![Rendered by QuickLaTeX.com \text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f68dce6e62d98d10d99daf57e0128069_l3.png)
![Rendered by QuickLaTeX.com \text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd1d3bbced66caaed0ac254363e5f2f1_l3.png)