本页解释了什么是反比例函数以及如何绘制它们的图表。此外,您还会发现此类函数的所有特征、如何计算其定义域以及逐步解决练习的几个示例和练习。
什么是反比例函数?
反比例函数是一种将两个反比例量相关联的函数,也就是说,一个量在另一个量减少时增加,反之亦然。一般来说,反比例函数由以下公式定义:
![]()
金子
![]()
是一个常数,称为比例比。
因此,反比例函数总是由分母为一次多项式的分数组成。因此,它们是一种有理函数。
反比例函数的示例:
![]()
一般来说
![]()
通常是自变量并且
![]()
因变量,或者换句话说,变量
![]()
取决于
![]()
另一方面,比例比(分子项)可以是正数或负数,其符号标志着函数的增加或减少:
- 如果常数

为负数,函数是递增的。
- 相反,如果常数

为正,则函数递减。
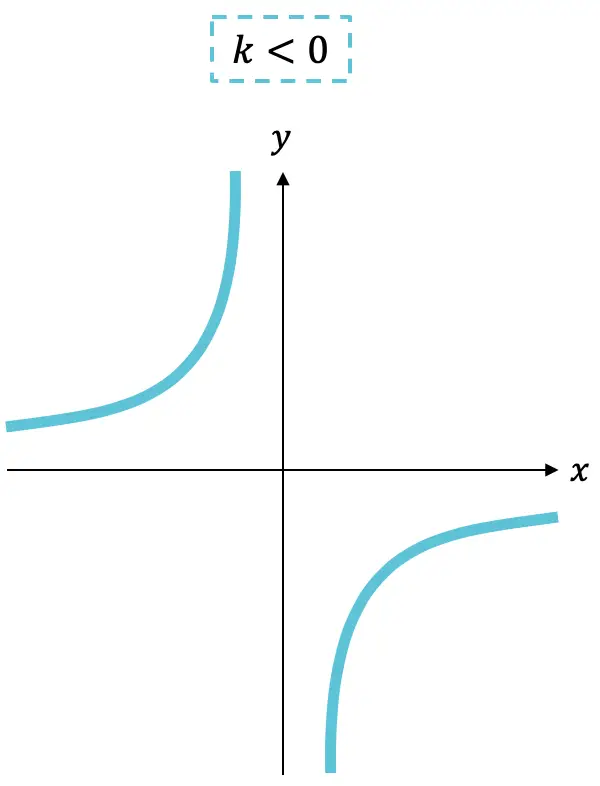
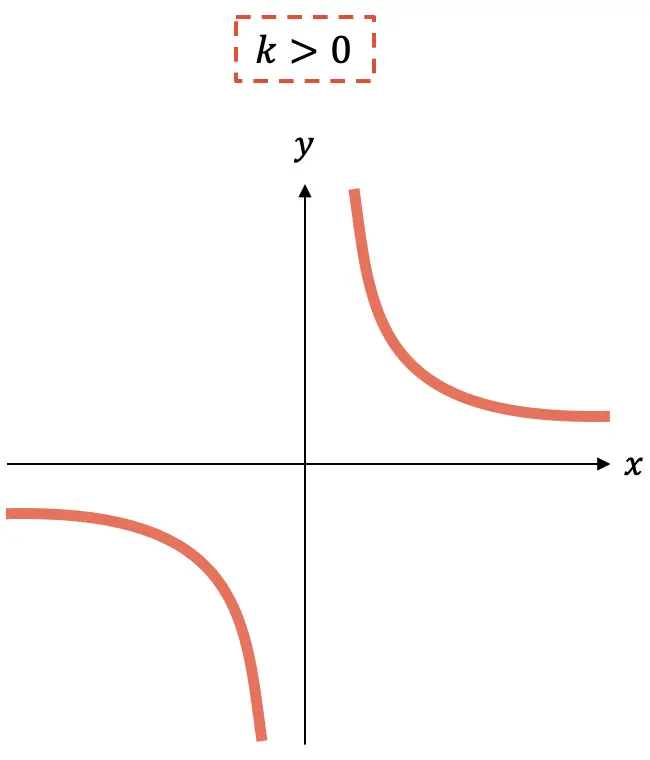
正如您所看到的,反比例函数的图形始终由两条双曲线组成,根据k的符号,它们将位于一个象限或另一个象限中。
反比例函数的域
作为一种有理函数,反比例函数的定义域是除分母中消失的实数之外的所有实数。因为分母永远不可能为零,否则会导致无穷大。
作为示例,我们将确定以下反比例函数的域:
![]()
要知道分母何时为零,我们必须将其表达式等于 0 并求解方程:
![]()
![]()
因此,当 x 取值为 1 时,分母将为零,我们将获得不确定性。所以函数的定义域是所有实数减去
![]()
![]()
如何绘制反比例函数的图像
我们将通过示例了解如何绘制反比例函数的图表。
- 我们将在图中表示以下函数:
![]()
我们需要做的第一件事是找到函数的定义域。作为分数,分母永远不可能为 0,因为那样会导致无穷大。因此,除非分母被取消,否则定义域将全部为 x。
因此,我们将分母设置为 0,以查看哪个 x 不属于该域:
![]()
![]()
因此,函数的定义域是除 2 之外的所有数字:
![]()
一旦我们知道哪个数字不属于该域,我们就创建一个值表。为了表示反比例函数,需要计算不属于域(2)的数左边的3或4个点和右边的3或4个点:
![]()

现在让我们在图表上表示点:
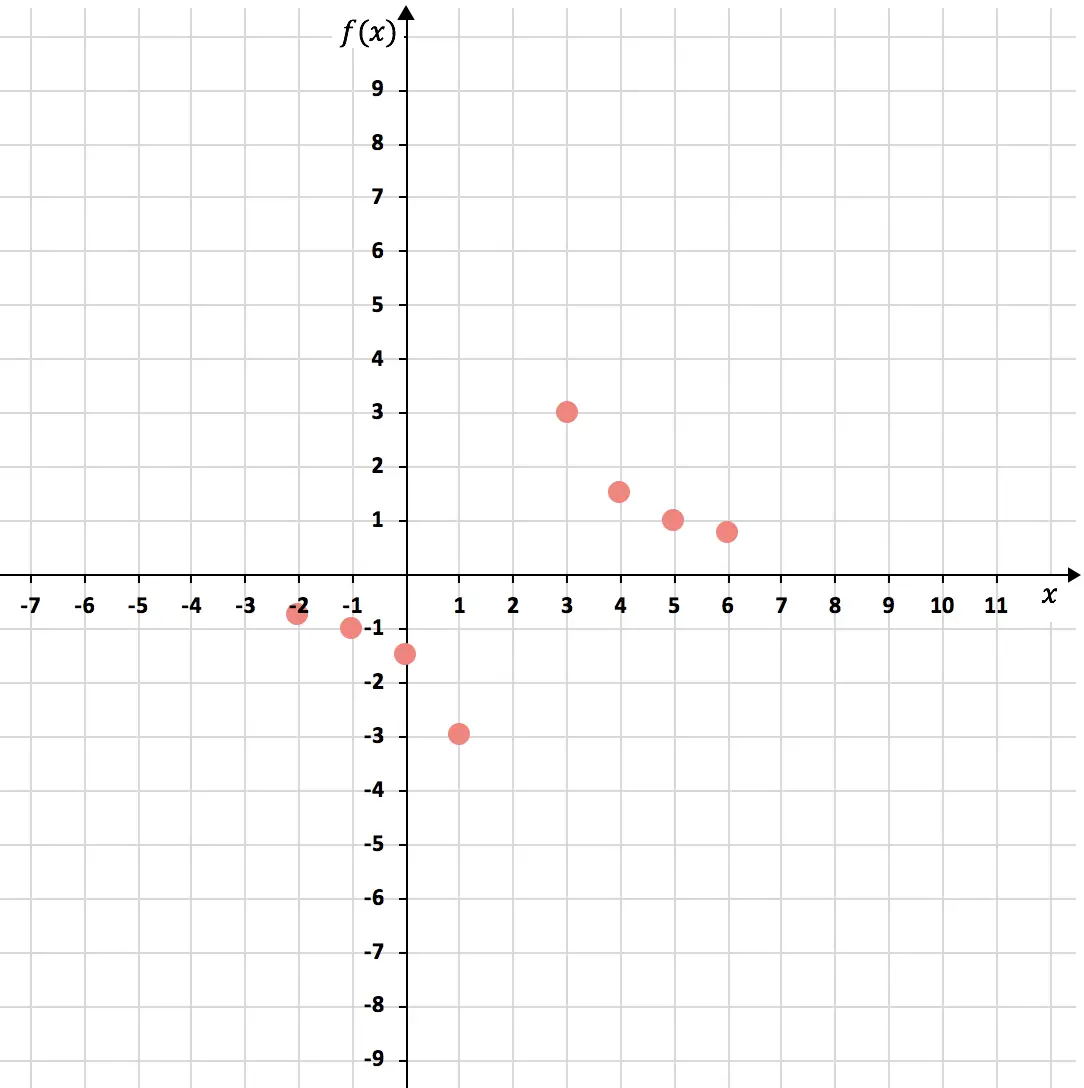
最后我们将这些点连接起来,形成反比例函数的两条双曲线。此外,我们延长双曲线的分支以表明它们继续增长:

请注意,该函数近似于
![]()
,在右侧和左侧。然而,它从未完全达到 2,它非常接近但从未达到 2。所以,
![]()
它是一条垂直渐近线。这是因为
![]()
不属于该函数的域,因此该函数在该点不存在。
水平 X 轴也会发生同样的情况。该函数近似为
![]()
但永远不要碰它。然而,
![]()
是一条水平渐近线。
这意味着所有反比例函数都是不连续的,因为它们总是有渐近线。
您可以在我们的网站上了解有关渐近线和函数极限的更多信息。
解决了反比例函数的问题
练习1
计算以下反比例函数的域:
![]()
当分母为 0 时,反比例函数将不存在,因为此时该函数将产生 ∞。因此,我们需要将函数的分母设置为0,才能看到x抵消了分母,因此不属于定义域。
![]()
![]()
![]()
![]()
练习2
绘制以下反比例函数的图像:
![]()
首先要做的是计算函数的域:
![]()
![]()
一旦我们知道哪个数字不属于该域,我们就可以使用以下函数创建一个值数组:

最后,我们将得到的点表示在图上并绘制双曲线,从而形成反比例函数:
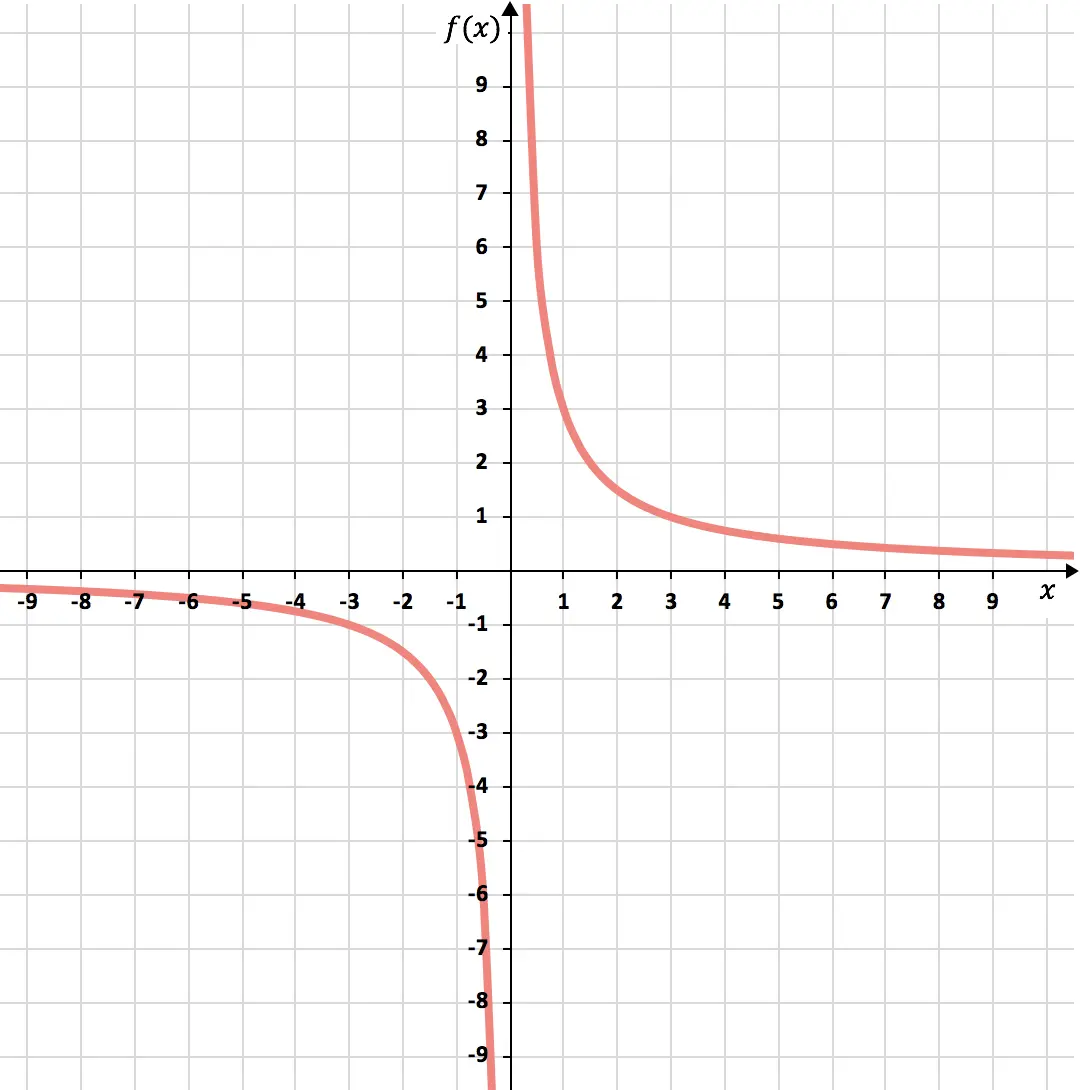
练习3
绘制以下反比例函数的图像:
![]()
首先要做的是计算函数的域:
![]()
![]()
![]()
一旦我们知道了函数的域,我们就构建一个值表:

最后,我们将获得的点表示在图表上并绘制双曲线,从而形成反比例函数:
练习4
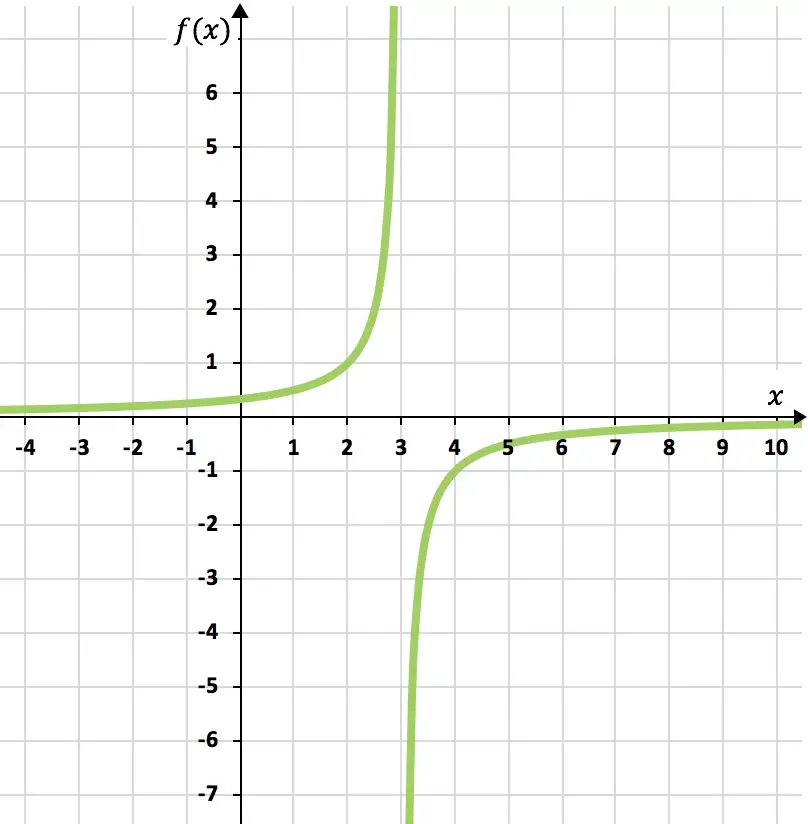
绘制以下反比例函数的图像:
![]()
首先,我们需要计算函数的定义域:
![]()
![]()
![]()
![]()
一旦我们知道了函数的域,我们就创建一个值数组:
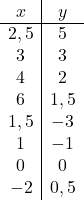
最后,我们将获得的点表示在图表上,并绘制双曲线,从而形成反比例函数:
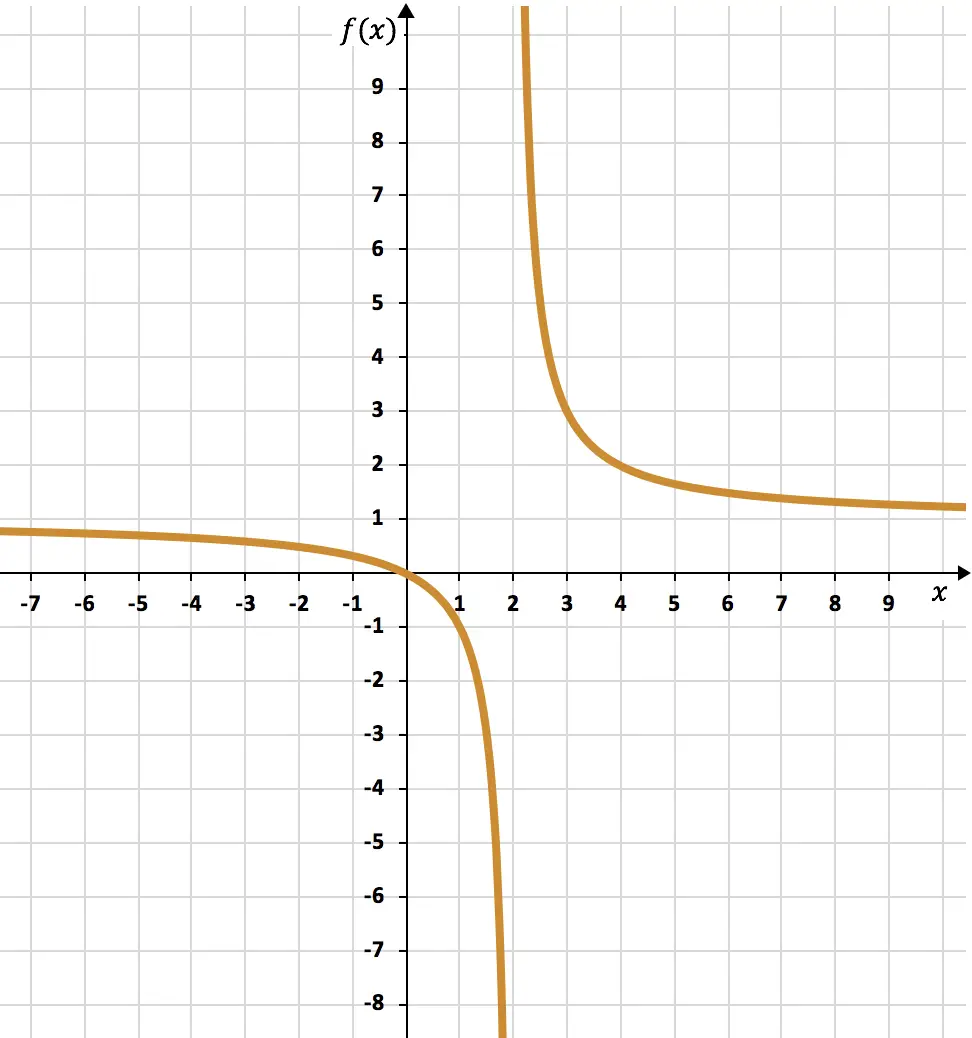
练习5
画出以下有理函数的图形:
![]()
首先要做的是计算函数的域:
![]()
![]()
![]()
![]()
一旦我们知道了函数的域,我们就构建一个值表:

最后,只需在图表上表示获得的点并绘制双曲线,从而形成分数函数:

反比例函数的应用
反比例函数在物理和数学中经常出现。
例如,它用于描述在恒定温度k下的理想气体中压力与体积之间的关系。该函数称为波伊尔-马里奥特定律 (P×V=k),是反比例函数的一个示例。显然,该函数的定义域仅限于正分支,因为不存在负体积或压力。
恒定电势差下的电流强度和电阻之间的关系也受反比例函数控制。该函数称为欧姆定律 (V=I×R)。