在此页面上,您将找到什么是幂零矩阵的解释,以及几个示例,以便您可以理解它并且毫无疑问。此外,您将能够看到幂零矩阵的结构以及这些类型矩阵的所有属性。
什么是幂零矩阵?
幂零矩阵的定义如下:
这个条件并不意味着无论指数如何,幂零矩阵的幂总是为零,而是如果存在至少一个矩阵的幂其结果是全0的矩阵,则该矩阵是幂幂的。
另一方面,幂零矩阵的幂零指数是满足幂零条件的最小数。我们也可以说幂零矩阵的阶数为k ,其中k是其幂零指数。
幂零矩阵的示例
为了完成对幂零矩阵概念的理解,我们将看到此类矩阵的几个示例:
2 × 2 幂零矩阵的示例
以下维度为 2×2 的方阵是幂零的:
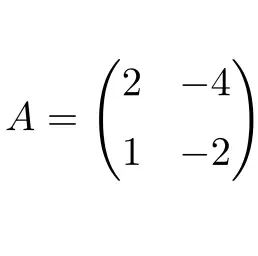
该矩阵是幂零的,因为通过对矩阵 A 求平方,我们得到零矩阵:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fde370dd31b0e2a533fdf1e9d23cf2c9_l3.png)
因此它是一个幂零矩阵,其幂零指数为2,因为获得零矩阵的二次方。
3×3 幂零矩阵的示例
下面的 3阶方阵是幂零的:
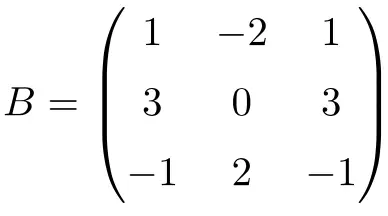
尽管将矩阵提高到 2 我们并没有得到零矩阵:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbad4ccc270e2960ae50cc23eacc7530_l3.png)
但是在计算矩阵的立方时,我们得到一个所有元素都等于 0 的矩阵:
![Rendered by QuickLaTeX.com \displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-da876a04b14d80c156e24c95bd22372e_l3.png)
所以矩阵B是幂零矩阵,并且由于得到的零矩阵是3次方,所以它的幂零指数为3。
2 × 2 幂零矩阵的结构
下面您可以看到所有幂零矩阵的结构。它的证明有点乏味,所以我们直接给你留下了获得 2 阶幂零矩阵的公式:
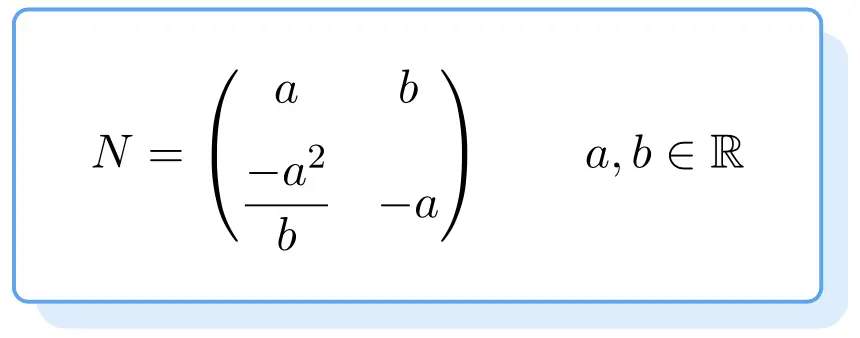
因此任何满足上式的矩阵都是幂零矩阵。为此,值
![]()
和
![]()
它们可以是任意的,只要它们是实数即可。
幂零矩阵的性质
幂零矩阵具有以下特点:
- 幂零矩阵的迹始终为零。
- 类似地,任何幂零矩阵的行列式始终为0。但是,反过来则不然,即矩阵的行列式为零并不意味着该矩阵是幂零的。
- 唯一可以对角化的幂零矩阵是零矩阵。
- 维度n×n的幂幂矩阵的幂幂指数始终等于或小于n 。这就是为什么 2 × 2 幂零矩阵的幂零指数始终为 2。
- 幂零矩阵是不可逆的。
- 任何主对角线上有零的三角矩阵也是幂零矩阵。
- 有一个定理说如果矩阵

是幂零的,那么矩阵
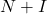
是可逆的,其中
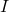
是单位矩阵。另外,其逆矩阵可由以下公式求得:
![]()
- 等价地,如果

是幂零矩阵,那么可以计算矩阵的逆
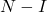
具有以下等式:
![]()
- 任何奇异矩阵,即不可逆矩阵,都可以分解为幂零矩阵的乘积。
- 幂零矩阵的所有特征值(或特征值)均为零。
![]()
- 最后,出于好奇,还有幂零变换的概念,它定义了线性应用
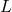
向量空间的
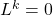
。