在此页面上,我们解释什么是幂等矩阵。我们还向您展示了此类矩阵的几个示例,以便您完全理解它。此外,您还将找到求幂等矩阵的公式,最后,找到幂等矩阵的所有属性。
什么是幂等矩阵?
幂等矩阵的定义如下:
幂等矩阵是指当其与其自身相乘时得到相同矩阵的结果。
![]()
因此,幂等矩阵的任何幂都等于矩阵本身,无论指数如何:
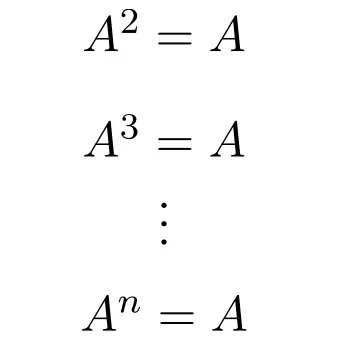
事实上,这就是这种类型的板得名的原因。因为在数学中,幂等性是一种运算,这意味着无论执行多少次,我们总是得到相同的结果。
幂等矩阵的示例
一旦我们了解了幂等矩阵的概念,我们将通过一些不同维度的例子来完成对它的理解。
2×2 幂等矩阵示例
以下维度为 2×2 的方阵是幂等的:
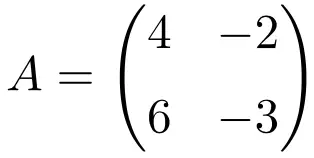
为了验证它是幂等矩阵,我们计算它的平方:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d83fda6875c8447818921c12f3196a7b_l3.png)
结果是相同的,因此我们证明它是一个幂等矩阵。
3×3幂等矩阵示例
以下大小为 3×3 的方阵是幂等的:
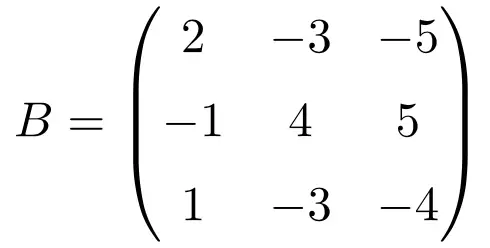
为了检查幂等矩阵是否对应,我们将矩阵提高到 2:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49a3f48608f3126039c949cde6346acf_l3.png)
结果与原矩阵相同,因此证明了矩阵的幂等性。
2×2 幂等矩阵的结构
这里我们向您展示获得幂等矩阵的公式。如果你更感兴趣,你可以在评论中看到下面公式的演示,但是有点繁琐,所以这里我们直接给你提供幂等矩阵的公式:

这样幂等矩阵的次对角线的元素可以是任意的,只要满足条件
![]()
主对角线上的数字必须是
![]()
和
![]()
除了这个公式描述的所有矩阵之外,我们还必须添加单位矩阵,它也是一个幂等矩阵,尽管它不遵守该公式。如果你不知道数组是什么,可以问Identity数组是什么。
幂等矩阵的性质
幂等矩阵具有以下特点:
- 幂等矩阵的行列式总是0或1。
- 除单位矩阵外,其他幂等矩阵都是奇异矩阵或简并矩阵,即不可逆。
- 任何幂等矩阵都是可对角化的,它的特征值(或多个特征值)总是0或1。
- 幂等矩阵的迹等于矩阵的秩。
- 最后,幂等矩阵和对合矩阵之间有一个关系:矩阵

是幂等的当且仅当矩阵
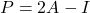
它是内合性的。