在此页面上,您将找到相似矩阵(也称为相似矩阵)的解释。此外,我们向您展示了两个相似矩阵的清晰示例以及此类矩阵的所有属性,以便您毫无疑问。最后,您甚至可以了解它们与全等矩阵的关系。
什么是相似(或类似)矩阵?
相似矩阵的定义如下:
两个矩阵
![]()
和
![]()
如果存在矩阵,则相似(或相似)
![]()
且满足以下条件:
![]()
或同等学历:
![]()
事实上,矩阵
![]()
充当基础变化矩阵。因此,这个方程的意思是矩阵
![]()
可以用另一个基数表示(
![]()
),这产生了矩阵
![]()
。
该术语也可以称为相似变换,因为我们实际上是在变换矩阵
![]()
在矩阵中
![]()
。
显然矩阵
![]()
它必须是正则或非简并矩阵(非零行列式)。
另一方面,我们可以表明两个矩阵类似于以下表达式:
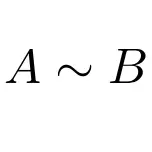
对于线性代数来说,这类矩阵比看起来更重要。它们主要用于可对角化矩阵,因为对角化任何矩阵的过程都是基于矩阵相似度的概念。
事实上,对矩阵进行对角化的过程涉及计算一个相似的矩阵,该矩阵同时也是对角矩阵。您可以在如何对矩阵进行对角化中了解它是如何完成的。
类似或类似矩阵的示例
然后我们将看到一个 2×2 维相似矩阵的例子来完成概念的吸收。
- 方阵 A 和 B 通过可逆矩阵 P 彼此相似:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4978e1117b69063b63256a0663eaf207_l3.png)
![Rendered by QuickLaTeX.com \displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6344f1d5a14dd381ab105bcb52827455_l3.png)
为了证明这些是相互相似的矩阵,我们必须首先计算 P 的逆矩阵:
![Rendered by QuickLaTeX.com \displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49a4a995246e782635e2e2b43302798_l3.png)
现在我们通过执行定义两个矩阵相似度的矩阵乘积来检查它们是否相似:
![]()
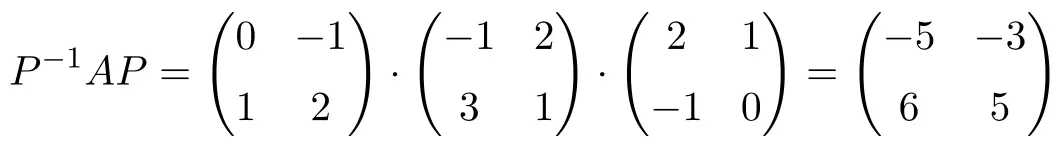
![]()
✅
是的,满足相似关系,所以它们是相似矩阵。
相似的矩阵性质
两个相似的矩阵 A 和 B 具有以下特征:
- 等级相同。
![]()
- 两个矩阵的行列式相同。
![]()
- 同样的追踪。
![]()
- 相同的 特征值(或特征值)。然而,特征向量(或特征向量)通常是不同的。
- 相同的特征多项式和最小多项式。
- 矩阵转置与原始矩阵类似。
- 可以通过对矩阵 A 的行应用初等运算来找到矩阵 B,反之亦然。
- 显然,相似性已经体现出来了。也就是说,如果A与B相似,则B也与A相似。
- 此外,矩阵的相似性也是对称的。换句话说,如果用矩阵 P 可以得到与 A(B) 相似的矩阵,那么用同样的矩阵 P 也可以得到与 B(A) 相似的矩阵:
![]()
![]()
- 此外,相似性是传递的。因此,如果矩阵 A 与矩阵 B 相似,矩阵 B 与矩阵 C 相似,则矩阵 A 也与矩阵 C 相似。
![Rendered by QuickLaTeX.com \left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9f845ee4a4c9e72220ecb4033ea9640_l3.png)
- 最后,每个模具都类似于锯齿模具。并且从这个性质我们可以推导出以下推论:每个方阵都类似于三角矩阵。
全等矩阵
另一方面,矩阵之间还有另一种非常相似的关系,但不是逆矩阵,而是转置矩阵。这就是所谓的一致性。
如果存在满足以下等式的可逆矩阵 P,则两个矩阵 A 和 B 是全等的:
![]()
正如您所看到的,这是相似矩阵的模拟,但矩阵转置了。