差值的平方（或减法）

在这里，我们解释什么是差（或减）的平方的著名恒等公式是什么，也就是说，我们向您展示如何求解表达式 (ab) ² 。此外，您将能够看到示例并练习解决差值平方的练习。最后，我们展示了这一非凡产品类型的公式演示和几何解释。

差值（或减法）的平方是多少？

差的平方或减法的平方是值得注意的恒等式（或值得注意的乘积）之一，也就是说，它由一条数学规则组成，该规则有助于计算具有两项的二项式的求积：一项是正数，一项是另一个负面的。

因此，差的平方的代数表达式是(ab) ² 。

差值平方公式（或减法）

一旦我们了解了这种显着恒等式的定义，我们就会看到如何用它的公式来求解差的平方：

因此，差值的平方等于第一项的平方，减去第一项与第二项乘积的两倍，再加上第二项的平方。

因此，要计算差值或平方减法，您不仅必须将每一项增加到 2，还必须将它们相乘并乘以 2。

记住这一点很重要，因为平方减法时一个非常常见的错误是不将乘积放在两项之间，而只求解减法的平方和减法的减法：

不要忘记 a 和 b 之间的乘积！

差（或减）平方的示例

现在我们知道了差平方的公式，我们可以用它进行计算。因此，您可以看到这是如何完成的，我们准备了几个差值（或减法）平方的已解决示例。

实施例1

• 求解以下差值平方：

这是一个平方减法，所以你必须应用它的公式：

所以，我们必须确定未知数的值是什么

和

的公式。在这种情况下，

是变量

和

对应数字3：

请注意，负号不是

但您必须始终采用不带符号的数字才能正确应用公式。

因此我们已经知道了

和的

因此，我们只需要将这些值代入公式即可：

实施例2

• 计算以下二项式的平方减法：

平方差的公式为：

所以，我们首先需要确定的值

和的

的公式。在这个问题中，

代表单项式

和

等价于二项式的独立项，即 2：

最后，一旦我们知道了参数的值

和

，我们简单地应用二项式公式进行平方减法：

差平方公式的证明

然后我们将推导出减法平方公式的来源。尽管您不必记住证明，但理解其背后的数学仍然很好。

如果我们从所有减法的二项式的表达式开始：

显然，之前的幂等于因子的乘积

乘以自身：

现在我们应用分配律将两个括号相乘：

我们只需将相似的项组合在一起即可完成公式的证明：

为了从数学上证明减法平方的公式：

奇怪的是，平方减法的二项式表达式的展开也称为完全平方三项式。

差值平方的几何解释

为了彻底理解差的平方的概念，我们将了解如何从几何上解释这个显着的等式。

看下面的正方形，其边长是

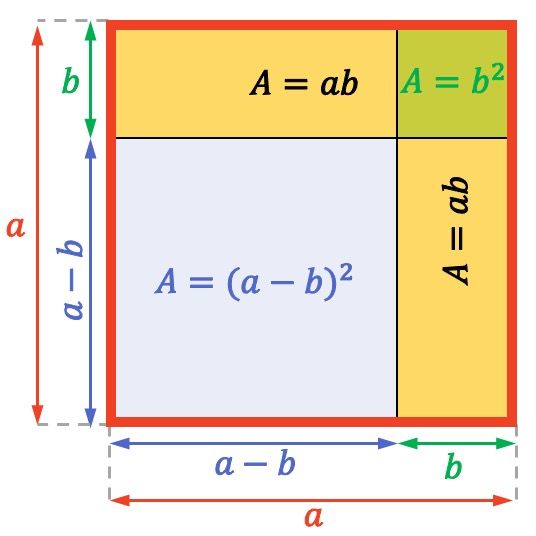
正方形或长方形的面积（或表面积）是通过将其两条相邻边相乘来计算的。因此，上面整个整数正方形的面积为

同样，每个黄色矩形的面积等于

最后，右上角显示的小正方形的面积为

这意味着一个正方形的边

其表面是

可以分解为一个维度的平方的面积

负 2 倍尺寸的矩形面积

和

，加上一个边长正方形的面积

简而言之，差的平方的公式也可以通过几何验证：

解决了差的平方（或减法）问题

为了方便您进行练习，我们为您提供了几个练习，逐步解决显着的差平方乘积。请记住，您可以在下面的评论中向我们写信您的任何问题。

练习1

解下列减法的平方：

练习2

应用以下公式确定以下两个量之差的平方：