在此页面上,您将看到什么是复数矩阵、共轭矩阵和共轭转置矩阵。现在他们看起来很像您,但您会看到在本页末尾您将完全理解每个人之间的差异。此外,我们还将看到每种类型及其属性的示例。
复矩阵
在看共轭矩阵和转置共轭矩阵的解释之前,我们先回顾一下复数矩阵的概念:
什么是复矩阵?
复矩阵是其元素之间具有一定复数的矩阵。
回想一下,复数或虚数是由实部和虚部组成的数字,用字母 i 表示。例如:
![]()
。
复杂矩阵的示例
让我们看一些复杂多维数组的示例:
2 × 2 阶复数矩阵示例
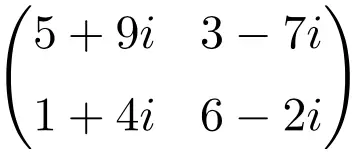
维度为 3×3 的复数矩阵示例
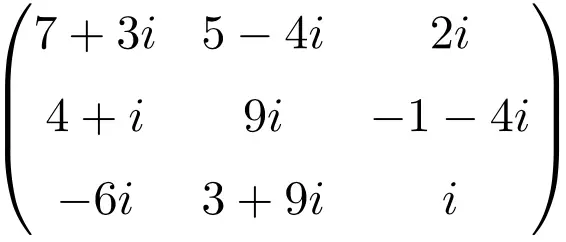
大小为 4×4 的复矩阵示例
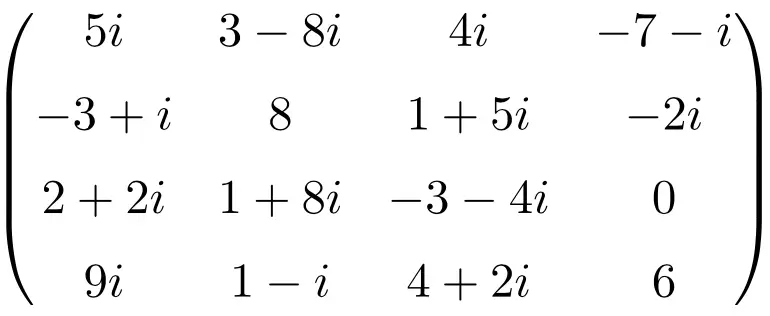
共轭矩阵
一旦我们了解了复矩阵的定义是什么,让我们看看共轭矩阵和转置共轭矩阵是什么:
什么是共轭矩阵?
共轭矩阵是一个复矩阵,其中它的所有元素都被它们的共轭取代,即它的所有复数的虚部的符号都被改变了。
共轭矩阵
![]()
用上面的横线表示:
![]()
。
共轭矩阵的示例
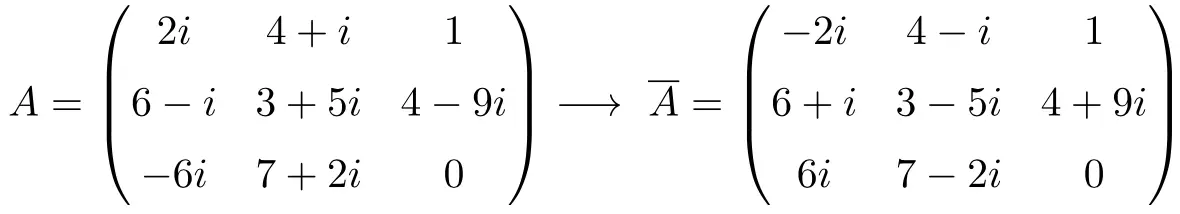
共轭矩阵的性质
此类矩阵的特点如下:
- 共轭矩阵的共轭就是原矩阵。
![]()
- 将两个矩阵相加(或相减)并共轭的结果与首先将两个矩阵分别共轭,然后将它们相加(或相减)的结果相同。
![]()
- 两个矩阵的共轭积等于两个矩阵分别共轭,然后计算矩阵乘法。
![]()
- 将矩阵乘以标量并对结果进行共轭与首先对标量和矩阵进行共轭,然后求解乘积相同。
![]()
- 转置矩阵然后共轭它意味着先共轭矩阵然后转置它。
![]()
- 对矩阵求逆然后对其进行共轭与对矩阵进行共轭然后对其求逆是相同的。
![]()
- 共轭矩阵的秩等于同一非共轭矩阵的秩。
![]()
- 计算共轭矩阵的迹或计算未共轭的同一矩阵的迹然后对结果进行共轭都没有关系。
![]()
- 最后,取共轭矩阵的行列式,计算未共轭的同一矩阵的行列式结果的共轭。
![]()
共轭转置矩阵
最后,在了解如何共轭矩阵之后,让我们继续讨论共轭转置矩阵的概念:
什么是共轭转置(或转置)矩阵?
转置(或转置)共轭矩阵是对一个矩阵进行转置然后使其共轭后得到的。
这类矩阵也称为伴随矩阵或简称为伴随矩阵。此外,它通常用星号表示
![]()
,尽管有些数学家把它画成
![]()
任何一个
![]()
。
共轭转置矩阵示例
下面是计算矩阵转置(或共轭转置)的示例:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
我们首先转置矩阵A:
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
然后我们计算转置的共轭矩阵,或者换句话说,我们改变所有复数的虚部的符号:
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
因此,共轭转置矩阵的计算总结为:
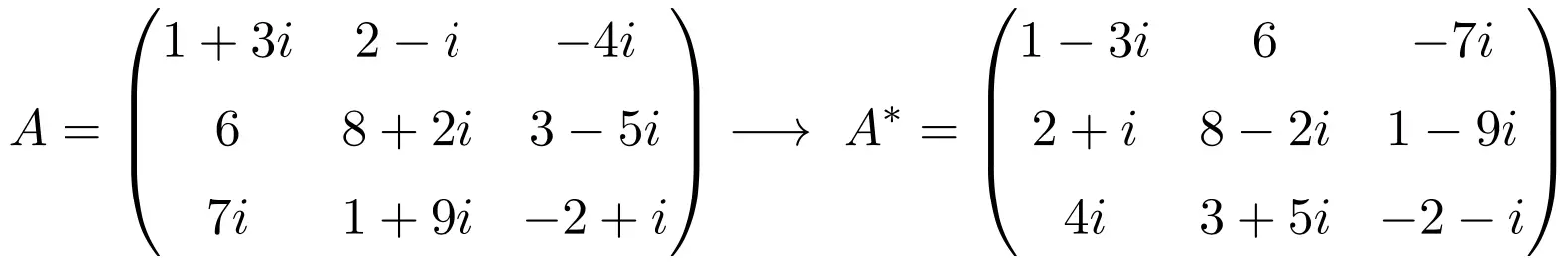
共轭转置矩阵的性质
此类方阵的性质如下:
- 先前转置共轭矩阵的共轭转置矩阵是原始矩阵。
![]()
- 共轭转置矩阵的加法性质表明,将两个矩阵相加(或相减),然后将此运算应用于结果相当于先对每个矩阵进行共轭转置,然后将结果相加(或相减)。
![]()
- 将两个矩阵相乘,然后进行共轭转置,得到的结果与共轭转置矩阵的逆积相同。
![]()
- 计算一个标量和一个矩阵的乘积的共轭转置矩阵与对复数进行共轭并分别求出矩阵的共轭转置然后相乘是一样的。
![]()
- 如果矩阵是可逆的,则矩阵求逆和共轭转置运算的执行顺序无关。
![]()