在此页面上,您将了解什么是共面(或共面)点以及如何知道某些点是否共面。此外,您将能够看到示例并通过已解决的共面点练习进行练习。
什么是共面点?
在解析几何中,共面(或共面)点的含义如下:
共面点是属于同一平面的点。
因此,2 或 3 个点总是共面,因为只需 3 个点即可形成一个平面。另一方面,当有 4 个、5 个或更多个点时,某些点可能不包含在同一平面中,因此它们不共面。
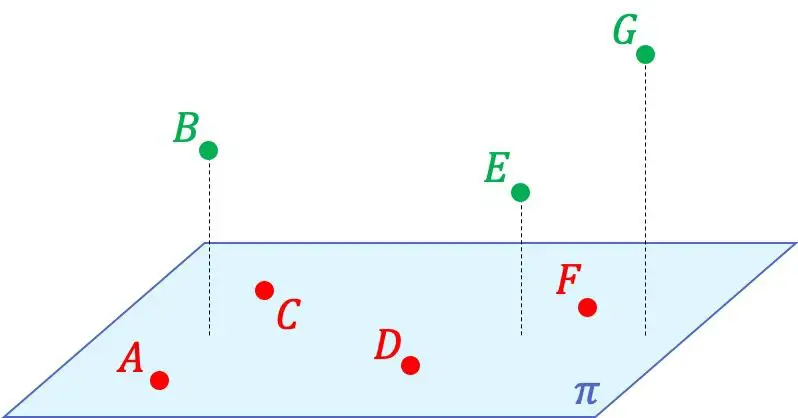
例如,在上面的图形表示中,您可以看到点 A、C、D 和 F 彼此共面,因为它们包含在同一平面中。另一方面,这4个点与B、E、G点不共面,因为在包含所有点的空间中无法形成平面。
从这个性质,我们可以推导出共面点定义的向量也是共面向量,即它们包含在同一平面内。
点什么时候共面?
正如我们在共面(或共面)点的定义中看到的,两个或三个点总是共面的,但超过三个点则不必遵守共面关系。
因此,判断四个或更多点是否共面主要有两种方法:
- 了解点是否共面的一种方法是通过点确定的向量:如果这些向量共面,则这些点也共面。
显然,要应用此方法,您需要知道向量何时共面。但由于还有多种方法可以确定一组向量是否共面,因此我们建议检查如何判断向量是否共面。在这里,您将找到查找 2、3、4 或更多向量何时共面的所有现有程序,以及示例和已解决的练习。
- 知道一组点是否共面的另一种方法是找到该组中3个点所形成的平面的方程,如果其他点满足该方程,则这意味着该组中的所有点都是共面的。
尽管这取决于问题,但我们建议使用这两种方法中的第一种,因为检查向量是否共面比计算平面方程要简单快捷得多。但是,显然,使用您喜欢的任何一个。
解决了共面点问题
练习1
判断以下三点是否共面:
![]()
![]()
![]()
在这种情况下,无需进行任何计算,因为3 个点始终共面,无论它们是什么。
练习2
判断以下四点是否共面:
![]()
![]()
![]()
![]()
为了使四个点共面,由它们确定的向量必须共面。因此我们计算这些向量:
![]()
![]()
![]()
现在让我们构造由向量形成的矩阵:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-873ec750665fdf215a648778d6fcf042_l3.png)
为了使结果向量共面,前一个矩阵的秩必须等于 2。为此,整个 3×3 矩阵的行列式必须等于 0:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-3eadb62f19c07b8a646fe9b2a00f9003_l3.png)
![]()
然而,整个矩阵的行列式不为零,因此矩阵的秩为3,因此4个点不共面。
练习3
判断以下五点是否共面:
![]()
![]()
![]()
![]()
![]()
为了使所有五个点共面,它们定义的向量也必须共面。因此我们计算这些向量:
![]()
![]()
![]()
![]()
现在让我们构造由向量组成的矩阵:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d571ea172dbf5e6b7d85da6db466eb0_l3.png)
为了使生成的向量共面,前一个矩阵的秩必须等于 2。因此,我们通过行列式计算向量矩阵的秩,以检查它们是否共面:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bec15883d9e3aa5a401afa41cd3992ae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd2f8cfa577e91b74c69e50cc36dfd9a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d551dddceb916cc6cf8bf4137903da1d_l3.png)
![]()
矩阵的秩相当于2,因此向量是共面的,因此5个点也是共面的。
练习4
计算参数值
![]()
使得以下 4 点共面:
![]()
![]()
![]()
![]()
为了使四个点共面,由它们确定的向量必须共面。因此我们计算这些向量:
![]()
![]()
![]()
其向量矩阵为:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
为了使所得向量共面,矩阵的秩必须为 2。因此,整个 3×3 矩阵的行列式必须为 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
最后我们解决了未知的问题
![]()
![]()
![]()
最后,如果本文对您有用,您可能还对如何计算两点之间的距离(公式)感兴趣,因为有时在解析几何问题中我们会被问到两点之间的距离是多少。在链接页面上,您将找到非常详细的解释,以及逐步解决的示例和练习。