计算两条线之间的交点或交点

在这里您将了解如何计算两条线之间的交点（或交点）。您还将看到示例，并且可以通过逐步解决的练习进行练习。

两条线之间的分界点或交点是什么？

两条线之间的交点（或切割点）是两条不同线相交的点。因此，当两条不同的直线有交点或交点时，就意味着它们重合于一点。

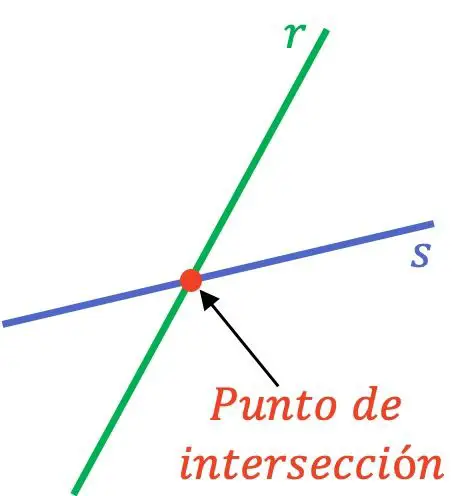
对于两条线相交于一点，它们必须是相交线，因为平行线不会在任何点相交。

如果您现在不记得什么是相交线，我们建议您查看我们的相交线示例页面，您可以在其中找到这些类型的线是什么以及如何判断两条线是否相交的详细说明。

如何计算两条线之间的截止点或交点？

一旦我们了解了两条线之间的交点或交点的定义，现在让我们看看如何计算该点。

要找到两条线之间的交点（或交点），首先必须确保两条线不平行，因为如果它们是两条平行线，则它们不会在任何点相交。因此，首先要知道如何判断两条线何时平行、何时不平行；如果您不记得如何操作，可以单击链接再次观看。

一旦我们知道两条线不平行，要确定两条线之间的交点（或交叉点），我们必须求解由每条线的方程组成的方程组。所述方程组的结果将是两条线之间的交点（或交叉点）的坐标。

如何查找两条线之间的交点或交点的示例

作为示例，我们将解决一个问题，以便您可以了解如何找到两条线之间的交点（或交叉点）：

• 找到以下两条线之间的交点：

首先，这些线不平行，因为它们具有不同的斜率，因此它们都相交于笛卡尔平面上的一点。

为了找到答案，我们必须求解由每行方程组成的方程组：

在这种特殊情况下，我们将通过均衡方法求解系统，因为两个未知数

已经解决了（两条线都是显式方程形式）：

我们删除变量的值

一旦你知道它值多少钱

我们将其值代入任何方程即可找到

则两条线的交点坐标为：

解决了两条线之间的交点或交点问题

练习1

下面两条线的交点或交点在哪里？

首先，两条线不平行，因为它们具有不同的斜率，因此两条线将在平面上的某个点相交。

为了计算该点，需要求解由每条线的方程组成的方程组：

在这种情况下，我们将通过均衡方法求解方程组，因为两个未知数

已经解决了（两条线都是显式方程形式）：

我们删除变量的值

一旦你知道它值多少钱

我们将其值代入任何方程即可找到

因此，两条线的交点坐标为：

练习2

找到以下两条线的交点或交点：

正确的

它以隐式（或一般）方程的形式表示，因此我们首先将其以显式方程的形式传递，以了解其斜率的值：

因此，这两条线具有不同的斜率，因此它们之间有一个交点。

为了计算该点，需要求解由每条线的方程组成的方程组：

我们用均衡法求解方程组：

我们删除变量的值

一旦你知道它值多少钱

我们将其值代入任一方程来找到

因此，两条线的交点坐标为：

练习3

确定以下两条线之间的交点或交点：

首先我们要知道这是否是两条平行线。为此，我们将查看两条线的方向向量是否成比例。

正确的

以参数方程的形式定义，因此其方向向量的分量就是参数前面的系数

另一方面，该行

以隐式方程的形式描述，故其方向向量为：

因此两个方向矢量的分量彼此不成比例，因此两条线不平行。

由于两条线不平行，这意味着它们之间确实存在一个交点。为了计算它，我们必须求解由每条线的方程组成的方程组：

在这种情况下，就像这一行

是参数方程的形式，需要将每个参数方程的表达式代入另一条线的方程中：

现在让我们求解所得方程：

并替换的值

查参数方程求出切割点坐标：

所以两条线的交点是：