在此页面上,您将找到有关右手定则(或定律)是什么以及如何使用它的说明。您还可以看到现有规则的 3 种变体,以及该规则的示例和实际应用。
什么是右手定则?
右手法则或定律,也称为螺旋法则,是一种用于确定矢量方向和方向的技术。也就是说,右手定则可以让你不用做计算就可以知道向量的方向和方向。主要用于查找两种运动的方向:线性运动和旋转运动。
以下是对右手定则的 3 种变体的解释:用三个手指、用手掌和开瓶器定则。这三个规则虽然不同,但目标相同,因此您只需要知道如何应用其中之一即可。经过三个解释后,您将找到右手定则的应用。
右手定则用3根手指
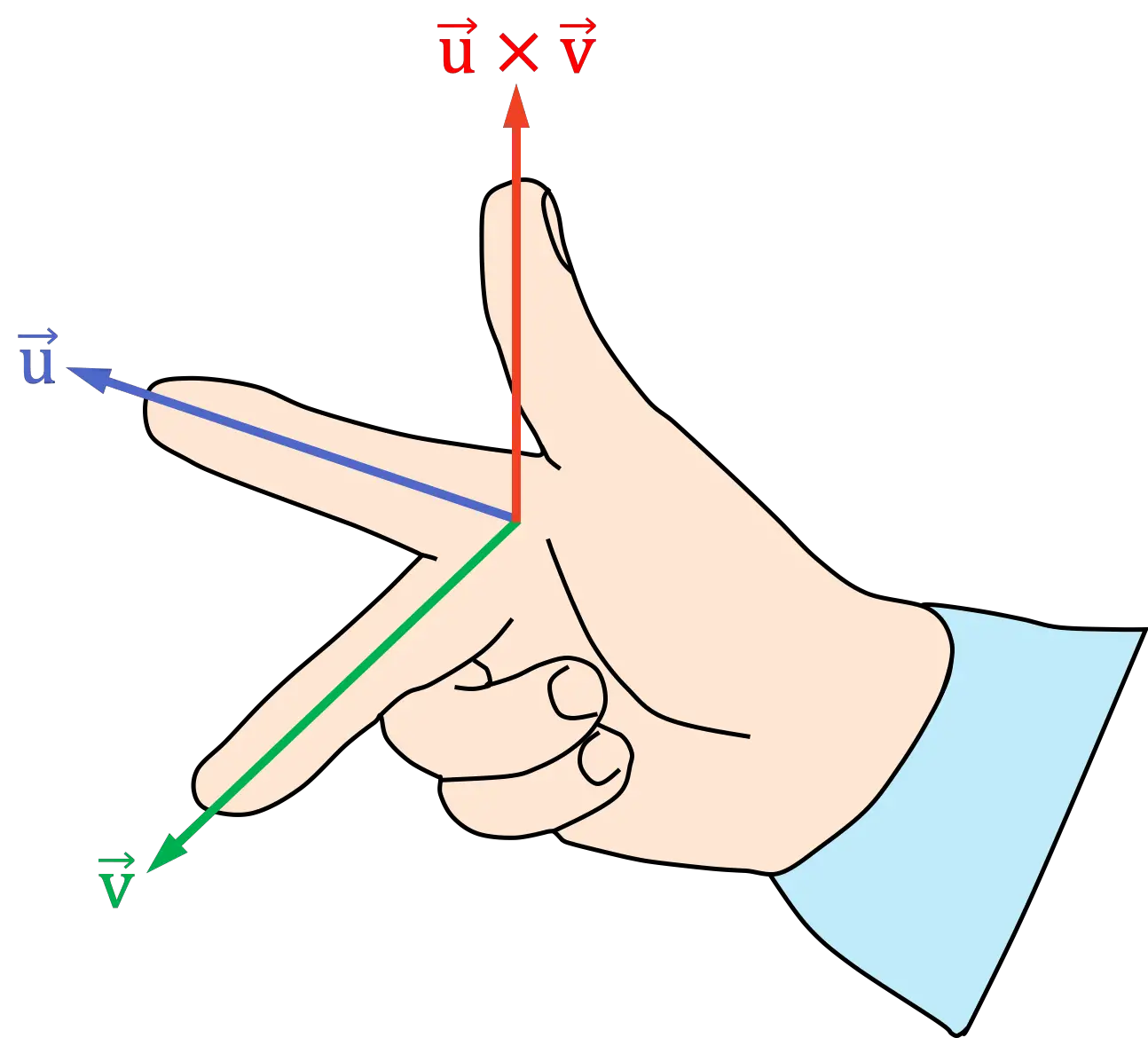
第一个版本的右手规则或法则是用3个手指完成的,用于求两个向量的向量乘积的方向和方向。因此,该规则由以下步骤组成:
- 将右手的食指放在叉积的第一个向量的方向上

- 将右手的中指(或中指)放在叉积的第二个向量的方向上

- 生成的拇指位置表示叉积的方向和方向

右手尺用整个手掌
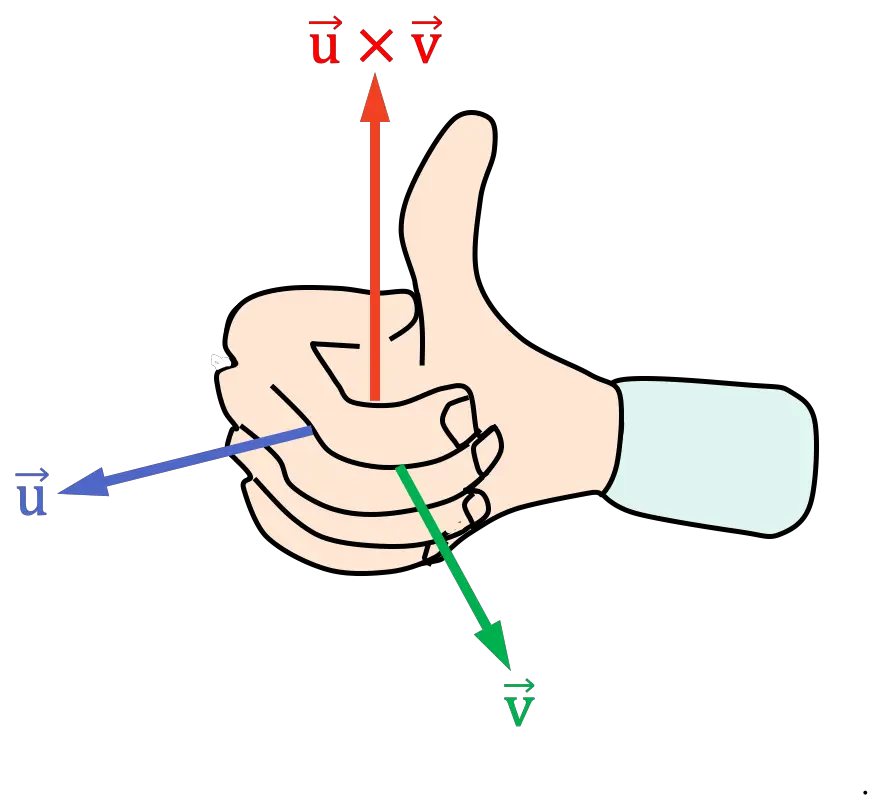
右手法则或定律的第二个版本用于整个手掌,也用于确定两个向量之间叉积的方向和方向。事实上,它与之前的变体类似。要应用它,您必须执行以下步骤:
- 将右手指向与叉积的第一个向量相同的方向

- 将手指移向叉积的第二个向量,合上右手

手应握在矢量之间的角度(或距离)最小的一侧。
- 拇指的最终位置决定了叉积的方向

开瓶器规则
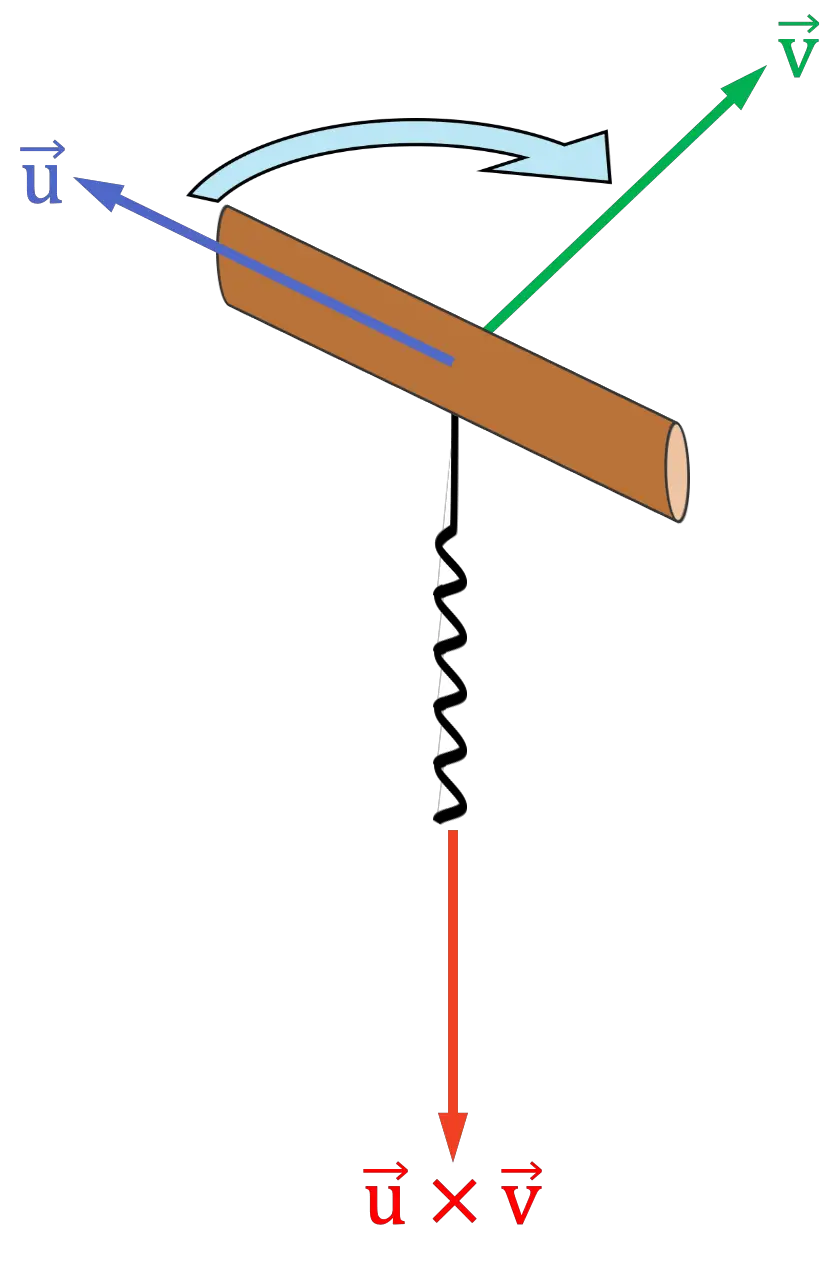
螺旋法则也可以用来知道两个向量之间向量积的方向和方向。其流程如下:
- 发挥你的想象力,放置一个开瓶器(或螺丝),其手柄指向与叉积的第一个向量相同的方向

- 然后将开瓶器转向叉积的第二个向量
就好像你要把它放进软木塞里一样。您需要将开瓶器转到向量之间的路径较小的一侧。
- 开瓶器螺旋指向的方向将是向量乘积的方向和方向

右手法则有什么用?
右手定则在数学和物理学中都有许多实际应用。下面我们向您展示最重要的一些。
磁场
在磁学中,右手定则用于计算磁场对带电粒子施加的力的方向,因为磁力公式中存在叉积。这就是所谓的洛伦兹定律:
![]()
金子
![]()
是磁力,
![]()
粒子的电荷,
![]()
其速度向量和
![]()
磁场矢量。
电磁场
在电磁学中,也使用右手定则,因为当一定强度的直流或交流电流流过导体(电缆)时,电缆周围会产生电磁场。因此可以使用右手定则找到该电磁场的方向:
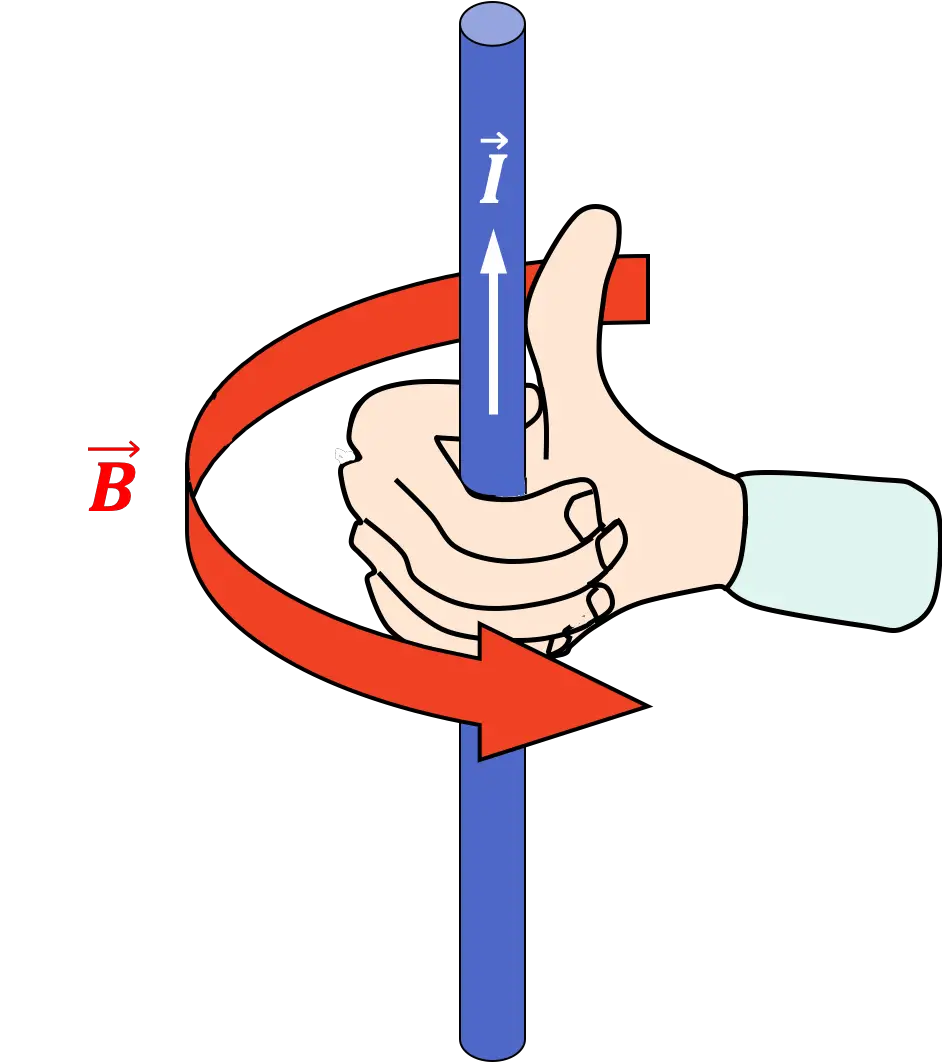
力量的瞬间
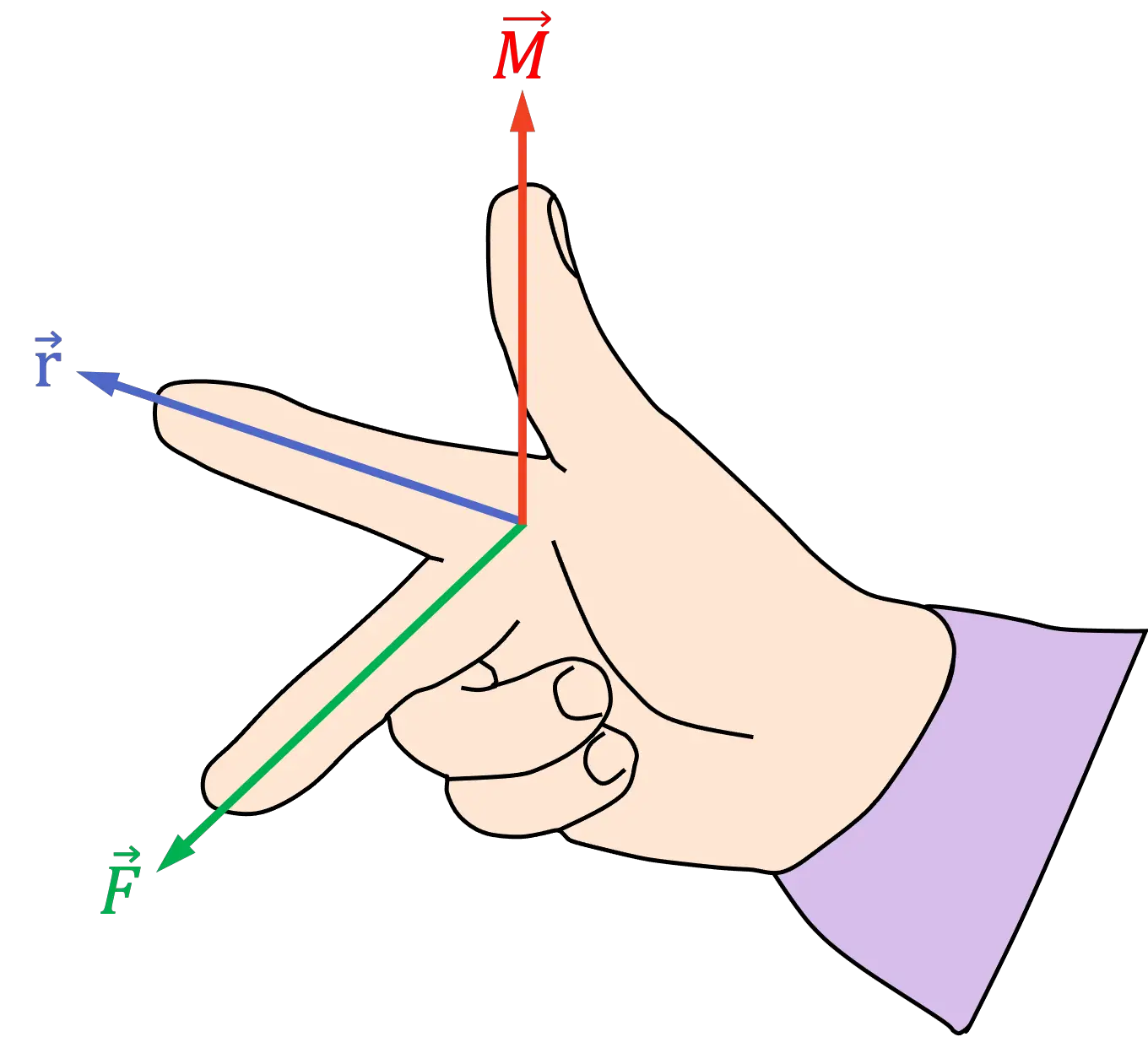
力的动量感在物理学中非常重要,特别是在力学中。使用右手定则可以轻松获得这个含义,因为矩量方程包含矢量积:
![]()
金子
![]()
是施加力产生的力矩
![]()
和
![]()
是力施加点与计算产生力矩的点之间的距离。
角速度
右手定理的另一个应用是确定角速度矢量的方向。要知道这个向量的含义,您需要用整个手掌使用正确版本的尺子。
如下图所示,如果物体顺时针旋转,则角速度矢量进入(负),而如果逆时针旋转,则角速度矢量退出(正)。

XYZ轴
最后,右手定则也可以用来表示任何三维参考系。因为如果你看右手法则中干预的3个手指(有3个手指),它们是相互垂直的,因此,它们也可以作为X、Y和Z轴的方向。