牛顿二项式是一个数学公式,用于表示两项的给定幂之和。这个公式以英国数学家艾萨克·牛顿的名字命名,被用于数学的许多领域。
例如,它在统计学、概率论以及微分和积分中具有实用性。二项式定理允许我们以简单的方式计算二项式的幂。
简而言之,牛顿二项式基于一个可以求解(a+b) n形式的代数表达式的公式。尽管这个公式是以艾萨克·牛顿的名字命名的,但值得一提的是,它的起源存在争议。
也就是说,一些研究表明二项式定理在中东的应用。
牛顿二项式是什么时候提出的?
牛顿二项式定理,又称牛顿二项式,于1665年提出,并于1676年在英国皇家学会官员的两封信中首次传达。
这些信件是对德国数学家戈特弗里德·威廉·冯·莱布尼茨的回应,他试图更好地理解对无限级数的数学研究。牛顿分享了他的定理结果,莱布尼茨认识到这是获得求积或级数结果的有用技术。
这一观察使牛顿得出结论:可以像处理有限多项式表达式一样处理无限级数。尽管牛顿从未发表过他的定理,但英国数学家约翰·沃利斯于 1685 年在他的《代数》中发表了该定理,并将其归功于牛顿的创造。
为什么叫牛顿二项式?
牛顿二项式以英国数学家和物理学家艾萨克·牛顿的名字命名,他在 17 世纪提出了它。牛顿并不是第一个发现该定理的人,但他是第一个证明该定理对于任何正整数 n 有效的人。
牛顿二项式是代数和微积分中非常有用的数学工具,广泛应用于物理、统计学、工程和计算机科学等领域。
牛顿二项式公式是什么?
正如我们之前提到的,牛顿二项式是可以求出二项式幂的公式。为了找到所述二项式幂,使用“二项式系数”。前一个术语指的是组合序列。
考虑到这一点,我们可以将牛顿二项式公式分解如下:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = a 3 + 3a 2 b + 3 ab 2 + b 3
涉及 (a+b) n展开的数学表达式称为显着实体,并且使得可以获得代表任何自然数“n”的该运算的通式。
通过检查每个所得多项式的系数,我们可以注意到遵循所谓的帕斯卡三角形的序列。
帕斯卡三角形的序列从数字 1 开始,在随后的每一行中,最后的数字始终为 1。通过将上一行中要计算的值正上方的两个数字相加来获得中间值。
如何找到牛顿二项式中的项?
要查找牛顿二项式中的特定项,请使用以下通用公式:
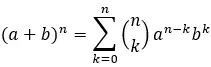
金子:
a 和 b 是二项式的系数。
n 是二项式的指数。
k 是我们要查找的特定项。
Σ表示k=0至n的总和。
[nk]为二项式系数,计算公式如下:
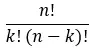
因此,完全展开的公式为:
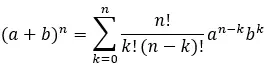
求解牛顿二项式的示例
一旦找到这些值,就将它们代入公式并求解表达式以获得特定项。例如,如果我们想找到二项式 (2x + 3) 6的第五项,我们将有:
一 = 2x
b = 3
n=6
k = 5
因此,使用以下公式:
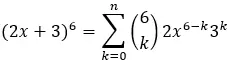
第五项对应于 k=5,因此我们有:
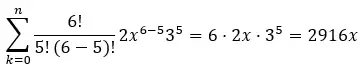
因此,二项式(2x + 3) 6的第五项是2916x。
什么是 5 次牛顿二项式?
5 次牛顿二项式是 (a + b) 5形式的代数表达式,其中“a”和“b”是变量,指数 5 表示二项式 的次数。展开这个表达式,我们得到一个有六项的二次多项式:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
该多项式的每一项都是通过将二项式的系数与“a”和“b”的幂相结合获得的。例如,第二项 (5a 4 b) 是通过将二项式系数 (5 选择 1 = 5) 乘以“a”的四次方和 b 的一次方得到的。
牛顿五次二项式在数学和物理学的不同分支中都很有用,例如统计学、概率论和量子力学。
牛顿二项式有哪些应用?
牛顿二项式在各个领域都有广泛的应用,包括:
- 计算概率:二项式定理用于计算二项式事件的概率,例如抛硬币或一系列测试的成功或失败。
- 数论——牛顿二项式用于展开多项式并简化数论中的方程。
- 统计:牛顿二项式用于计算二项式分布和构建置信区间。
- 物理学– 在物理学中,二项式定理用于相对论和量子力学等领域。
- 经济和金融:牛顿二项式用于计算一段时间内现金流的当前和未来价值以及金融期权的估值。
- 编程和计算机科学:牛顿二项式用于算法开发和计算机编程。
为什么牛顿二项式很重要?
牛顿二项式是相关的,因为它是代数和数论发展的基本数学工具。它允许您计算二项式的平方或任何其他幂的结果,这对于求解方程和简化代数表达式非常有用。
此外,它在统计、概率和物理学等领域也有应用。总之,牛顿二项式是数学中的一个基本概念,理解它对于许多研究领域的进步至关重要。
还有其他方法来表达牛顿二项式吗?
是的,还有其他方法来表达牛顿二项式。例如,它可以使用组合符号以二项式系数来表达。
此外,它还可以使用欧拉公式用指数函数和三角函数来表示。同样,在伽马函数方面使用勒让德公式。这些替代表达式在不同的上下文和数学问题中可能很有用。
牛顿二项式示例
然后让我们看一些牛顿二项式应用的简单例子。
示例 1:计算 (x + y) 5展开式中的 3 阶项。
解: (x + y) 5展开式中,第一项系数为1,第二项系数为5,第三项系数为10,第四项系数为10,则第五项的系数为5,第六项的系数为1。
因此,3 阶项为:
10x 2和3
示例 2:求 (2x – 1) 4展开式中的独立项。
解:在 (2x – 1) 4的展开式中,独立项在组合 (2x) p (-1) (4-p)中找到,其中 p 是 (2x) p的指数值, (-1) (4-p)加起来是 4。
因此,独立项是:
(2x) 2 (-1) 2 = 4
示例 3:查找 (3x – 2y) 6展开式中的最高次项。
解: (3x – 2y) 6展开式中的最高次项可在组合 (3x) p (-2y) (6-p)中找到,其中 p 是 (3x) p的指数值, (-2y) (6-p)等于二项式的次数,即 6。
因此,最高次数项是:
(3x) 3 (-2y) 3 = -216x 3和3