在这里您将了解如何求解三角极限。您将能够看到三角函数极限的几个示例,甚至可以通过解决三角函数极限的分步练习进行练习。
什么是三角极限?
三角极限是根据三角函数计算的极限。为了解决三角极限,必须应用初步程序,因为它们通常会引起不确定性。
此外,三角函数的无限极限不存在,因为它们是周期函数。也就是说,它的图表不断周期性地重复,而不趋向于特定值。
三角极限公式
所有三角极限均通过以下两个公式计算:
![]()
如果我们尝试通过替换来计算极限,我们会得到零之间的零不确定性:
![]()
但这个三角公式可以通过计算更接近的函数值和更接近x=0(以弧度表示的角度)来证明。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
三角函数的两个横向极限为 1,因此 x=0 点处的极限为 1:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
因此,当 x 趋于 0 时,x 的正弦除以 x 的三角极限等于 1。
这个公式也可以应用于多个角度:
![]()
![]()
如果我们尝试通过直接替换来求极限,我们会得到零之间的不定形式零:
![]()
但我们可以从上面的公式来检验是否相等。为此,您必须首先将分数的分子和分母乘以 1 加上 x 的余弦:
![]()
现在我们在分数的分子中有显着的恒等式,因此我们可以简化它:
![]()
![]()
从基本的三角恒等式开始,我们重写分子:
![]()
![]()
因此,我们可以将分数转换为分数的乘积:
![]()
![]()
利用极限的性质,我们可以将上面的表达式转换为极限的乘积:
![]()
使用上面演示的公式,我们可以轻松简化三角极限:
![]()
![]()
![]()
最后,我们计算结果极限:
![]()
因此,三角极限公式得到验证:
![]()
与其他公式一样,它也可以用于多个角度:
![]()
因此,要求解三角极限,就必须用算术对函数进行变换,得到类似的表达式。这样我们就可以使用两个公式之一并找到极限值。
另一方面,有时我们可能需要应用某些三角恒等式,因此我们将以下所有公式留给您
连接三个主要三角比率的公式:
![]()
基本三角恒等式:
![]()
由基本三角关系导出:
![]()
![]()
对角:
![]()
![]()
![]()
两个角度之和:
![]()
![]()
![]()
两个角度之差:
![]()
![]()
![]()
双角:
![]()
![]()
![]()
半角:
![]()
![]()
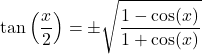
正弦和余弦的加法和减法:
![]()
![]()
![]()
![]()
正弦和余弦的乘积:
![]()
![]()
![]()
为了让您能够准确地了解三角极限是如何计算的,我们在下面整理了一个分步示例。
三角极限示例
让我们看看如何使用以下示例求解三角极限:
![]()
尝试计算三角极限,我们得到零与零之间的不确定性:
![]()
➤请参阅: 零之间的零限制
因此需要对三角函数进行变换来求解极限。正切函数等于正弦除以余弦,因此:
![]()
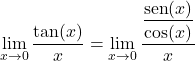
现在我们可以通过应用分数的性质将函数表示为乘积:
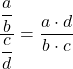
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
利用极限的性质,我们可以将两个相乘函数的极限转换为两个极限的乘积:
![]()
正如我们上面所展示的,第一个三角极限给出 1:
![]()
![]()
因此只需进行以下计算:
![]()
解决了三角极限的练习
练习1
求解以下三角极限:
![]()
首先,我们尝试通过直接求值来计算三角极限:
![]()
但我们的不确定性为零。所以我们需要对函数进行变换。
首先,我们将通过执行以下操作将 x 保留在分母中:
![]()
现在我们将分数乘以 4 并除以 4,得到一个表达式,可以应用第一个三角极限公式:
![]()
最后,我们应用一开始看到的公式来求解三角极限:
![]()
![]()
练习2
计算以下三角极限:
![]()
首先,我们尝试找到三角极限:
![]()
但不定形式“零”对应于“零”已达到。
然后,我们将正切转换为正弦和余弦的商:
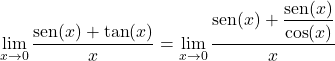
我们乘以和除以 x 的余弦:
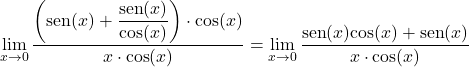
我们在分子中取一个公因数,然后将三角极限一分为二:
![]()
最后,我们求出三角极限的结果:
![]()
练习3
当 x 接近零时,求解以下三角函数的极限:
![]()
通过直接计算,我们得到 0 之间的不确定极限 0:
![]()
因此,我们将每一项除以 x 的正切来简化极限:
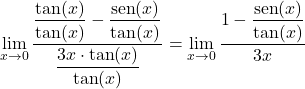
其次,我们可以从基本三角恒等式推导出分子的分数等于 x 的余弦:
![]()
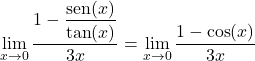
并且应用三角极限理论中演示的第二个公式,我们可以轻松求解极限:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
练习4
求下列三角极限在点 x=0 处的解:
![]()
如果我们尝试求解极限,我们会找到不定形式 0/0:
![]()
分子的代数表达式可以使用双角正弦的三角恒等式重写:
![]()
![]()
现在让我们将三角函数的极限分解为乘积:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
最后,我们通过应用极限的性质来求解三角极限:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)