在本文中,我们将回顾理解完整多项式所需的概念。此外,我们将了解它的使用方式以及为什么它对于操纵和量化多项式如此重要。不过,首先,强烈建议阅读我们关于多项式的文章。
什么是完全多项式?
完全多项式是由各项之和组成的代数表达式。每一项都是通过将一个数字(称为系数)乘以 x 的幂而形成的。多项式中的最高幂称为多项式的次数,最低幂(x 升为零)称为独立项。
从这里开始,我们将完整多项式定义为包含直到多项式 的次数为止的所有可能次数的项。换句话说,如果多项式的次数为 5,则它必须包含次数为 5、4、3、2、1 和 0 的项。换句话说,完全多项式是没有空项(等于 0)的多项式。 )。
在下图中,您可以看到一个示例。可以看出,在独立项中,x 的每个指数都有一个项,从 x 的 4 次方(4 是多项式的次数)到 x 的 0 次方。因此,该多项式满足完全多项式的定义。
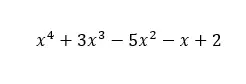
另一方面,如果我们有另一个多项式,如下图所示,我们将处理一个不完整的多项式。由于缺少两项,因此 x 的项提升为 2 和独立项。而从完备多项式的定义来看,只要缺少一项,多项式就不再完备。
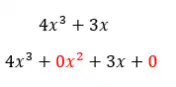
完全多项式的例子
现在您已经知道了完整多项式的定义,让我们看一些现实世界的示例。我们将从查看 2 次完全多项式开始,再查看另一个 4 次多项式,最后查看一个 6 次多项式。显然,我们可以给出更高次数的示例,但这个想法对于所有类型的多项式都是相同的。
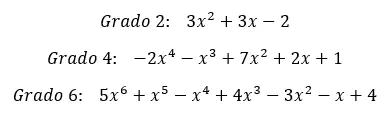
通过这些例子,完全多项式的定义非常清楚。这就是为什么我们现在可以进入下一个阶段。在下一节中,我们将根据项的顺序详细介绍存在的两种类型的完全多项式。这是很多学生认为理所当然的事情,但很高兴再次看到它。
完全多项式的类型
我们可以将完备多项式分为两类:有序完备多项式和无序或无序完备多项式。第一个特征是其项根据 x 的阶数排序的结构。从最高学位开始,以“独立”一词结束。
虽然它是一个完全无序多项式,但它是用随机顺序的项来表示的。因此,您可以找到独立项旁边具有最大指数的项。但是,这种表达多项式的方式并不实用,因此我们建议您始终使用有序多项式。
接下来,我们将向您展示每种类型的示例,以便您可以充分理解其中的差异。
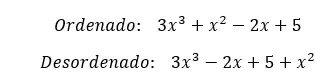
我们希望本文可以帮助您理解完全多项式的概念。如果您有任何疑问,请随时在评论中留下。