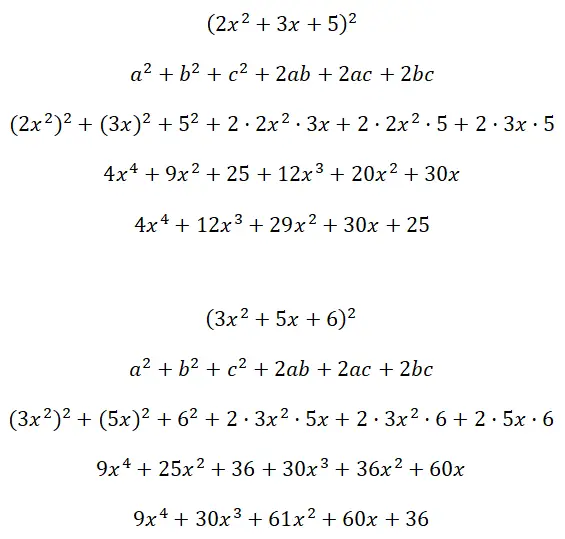什么是卓越的产品或卓越的身份?
显着恒等式,也称为显着乘积或显着等式,是可以更快地求解多项式的乘积和商的数学资源。正如“恒等”一词所表明的那样,这些等式使我们能够计算这些运算而无需求解它们。因为我们知道这个表达式遵循固定的规则(总是满足的),因此,我们可以得到结果而不必检查它。
何时使用显着身份?
这些恒等式主要用在代数领域,它们的主要功能是加速某个多项式的求解,而不必求解整个运算本身。从那里,我们获得了著名产品的配方,我们将在整篇文章中对其进行评论。最后,我们可以将公式应用于完整平方、因子多项式或任何其他类型的计算。
如何一步步解决出一款卓越的产品?
为了解析显着的身份,您需要遵循一个非常简单的过程,这也很有意义:
- 识别显着身份的类型:第一步是识别操作的类型:显着产品或显着商。您还应该澄清您需要应用什么类型的公式,尽管稍后我们解释了不同类型的显着恒等式后您就会理解这一点。
- 应用公式:一旦知道需要应用哪个公式,就可以进行计算了。根据身份的类型,您将必须解决或多或少复杂的运算,并且在绝大多数情况下,这些计算将由包含至少一个未知数的项组成。
- 简化表达式:最后,当得到结果时,需要对其进行简化。在此步骤中,您需要对相似的项进行分组并对它们进行排序以形成结构良好的结果多项式。应该注意的是,这一步与其他步骤一样重要,否则练习仍然不完整。
显着身份或主要显着产品的公式
您将在下面找到与著名恒等式相对应的所有公式。除了每个案例的理论解释外,还有一些值得注意的已解决的产品示例,通过它们您将更好地理解所有概念。值得一提的是,在第一部分中您只会找到最重要的身份。但是,通过阅读本文,您将学习如何开发更复杂的著名产品,例如由三项式组成的产品。
总和的平方
第一种情况涉及和的平方,这是代数领域中非常常见的多项式表达式。这可以写为: (a + b) 2 ,相当于: (a + b) · (a + b)。因此,我们知道可以使用多项式乘法来求解。但是,由于显着的恒等式,我们可以通过使用以下公式来节省时间: (a + b) 2 = a 2 + 2ab + b 2 。接下来我们给大家演示一下刚才看到的公式,这样大家就能明白它的出处和使用方法了:
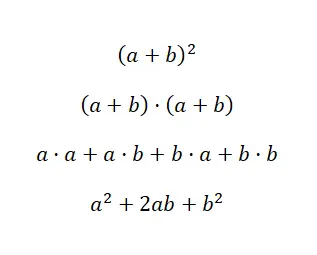
正如我们所看到的,我们使用之前评论过的多项式乘法进行了验证。我们可以绝对肯定地说,如果您熟记结果公式,那么通过执行简单的值替换,您可以更快地得到结果。所以这是一个非常有用的数学概念。现在您已经了解了总和的平方是如何计算的,我们将向您展示一个具体的示例:
总和的平方示例
计算显着恒等式 (2x + 4) 2 :
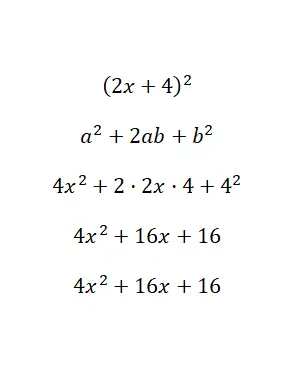
基本上,我们将二项式的值与公式的字母相关联,并求解:a = 2x 和 b = 4。最后,在求解完所有计算后,我们得到多项式 4x 2 + 16x + 16,即相当于原来的.在此示例中,我们从简化多项式获得了扩展多项式(标准形式)。
减法的平方
另一个非常常见的表达式是减法的平方,它很像加法的平方,只是改变了一个符号。那么,二项式的结构就等价于: (a – b) 2 ,如果我们展开它,我们得到: (a – b) · (a – b)。与前面的情况一样,这可以通过多项式的乘法来计算,尽管它还有一个有助于解决问题的公式:a 2 – 2ab +b 2 。您可以在下面找到这方面的经验证明:
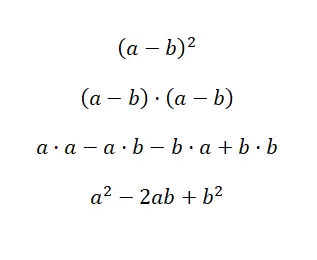
为了简化求差平方的过程,我们可以使用与平方和相同的公式,但第一个符号为负。这种最小的变化允许表达式适应由正项和负项组成的二项式,这对于减法很有用。现在我们将向您展示一个已解决的示例:
减法的平方示例
计算显着恒等式 (x – 3) 2 :
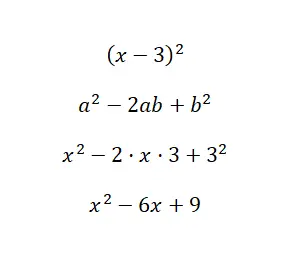
正如您在示例解决方案中看到的,我们将二项式的值代入公式中,a = x 和 b = 3。因此,使用我们之前解释的公式,我们只需要进行替换和一些非常基本的操作计算。这使我们能够看到使用该表达式计算差值的平方是多么容易。
平方差或差之和
显着乘积的第三种情况称为平方差,它由正二项式和负二项式的乘积形成。这种风格的表达式具有以下结构: (a + b) · (a – b),因此如果我们展开该乘积,我们将得到使计算更容易的公式:a 2 – b 2 。正如您所看到的,这是一个非常简单的公式,尽管要完全理解它,您需要进行所有计算:
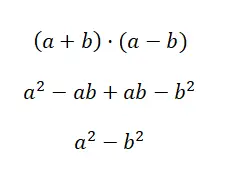
求和除以差的示例
计算显着恒等式 (x + 1) · (x – 4):
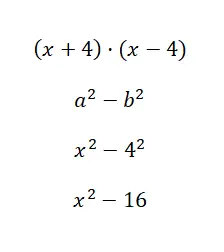
这次的数值计算非常简单,实际上我们只需要求解幂即可。尽管该公式确实仅适用于二项式具有相同的主项和相同的独立项但符号发生变化的情况。因此,这一身份很重要,但它不是您最常使用的身份。
具有共同项的两个二项式的乘积
在第四种情况下,我们发现自己面临的情况与前一种情况非常相似,尽管结构略有修改。观察我们向您展示的差异:(x + a) · (x + b) 和 (a + b) · (a – b)。如果您仍然不太清楚,请考虑以下示例:(x + 4) · (x + 5) 和 (x + 4) · (x – 4)。在第一种情况(两个公共项二项式的乘积)中,只有一个共享项,而在第二种情况(差之和)中,这两个项是公共项,但独立项有倒号。也就是说,让我们看看我们可以使用什么公式:
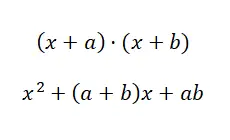
具有共同项的两个二项式的乘积示例
求解显着乘积 (x + 2) · (x + 3):
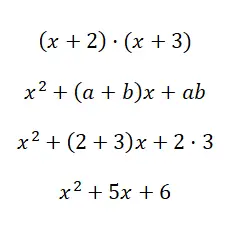
使用 x 2 + (a + b)x + ab 的公式,我们可以计算两个二项式相乘得到的二次多项式。我们希望通过这个例子您已经理解了我们解释的最后两种情况之间的区别,因为有时很难区分它们。
三项式的平方
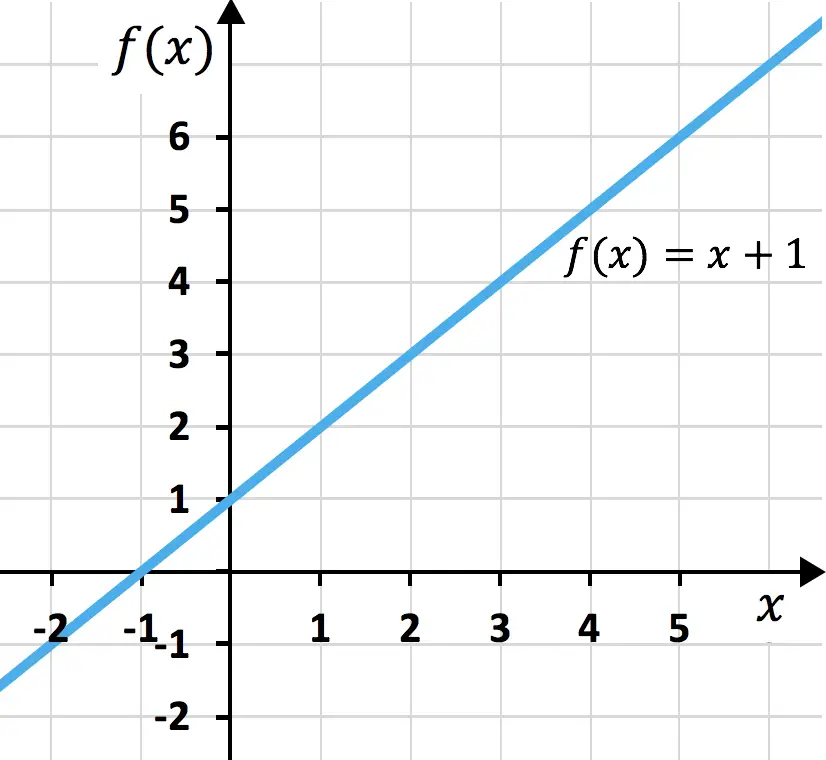
当我们尝试计算三项式的平方时,我们还有一个出色的产品可以让我们的生活变得更轻松。该表达式表示如下:(a + b + c) 2 ,等效乘积为:a 2 + b 2 + c 2 + 2ab + 2ac + 2bc。需要注意的是,这在正三项式的情况下有效,但如果其中一个系数为负,则只需将负值写入公式即可。下面是公式的演示:
三项式的平方示例
计算显着恒等式 (2x + 1 + x 2 ) 2 :
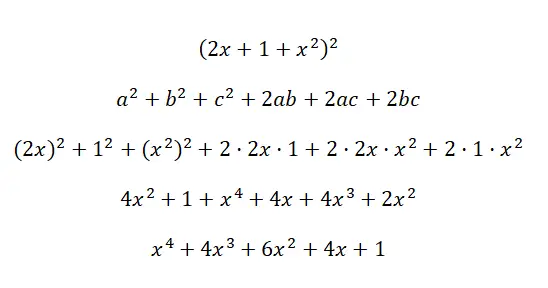
卓越的身份公式或卓越的立方产品
现在我们已经解释了主要的值得注意的恒等式,我们将看看它们的导数,从二项式的三次方开始。为了计算这种风格的著名产品,我们将不得不求助于稍微复杂一点的公式,但其结构与我们已经讨论过的类似。
二项式立方
二项式的立方写为: (a + b) 3和 (a – b) 3 ,该表达式等价于以下公式: (a 3 + 3a 2 b + 3ab 2 + b 3 ),和 (a 3 – 3a 2 b + 3ab 2 – b 3 )。这两种情况称为和的立方和减法的立方,因为它们是立方二项式。下面您将看到每个案例的非常详细的演示:
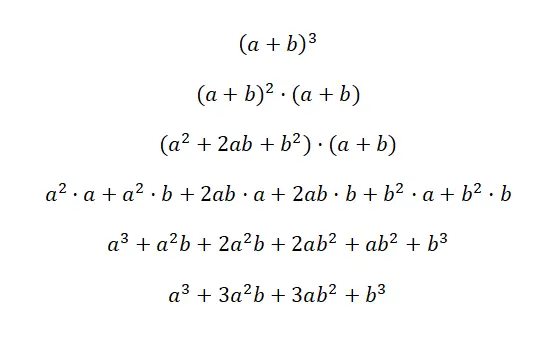
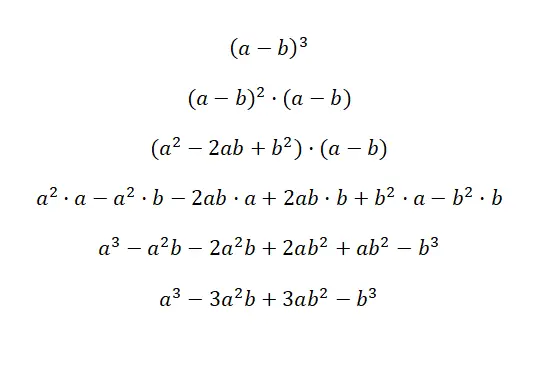
理解第一个证明的关键是理解 (a + b) 3等价于: (a + b) 2 · (a + b)。这样,我们就可以使用之前解释过的和的平方公式来乘以另一个因子。然后我们简单地简化表达式,得到相应的显着恒等式:a 3 + 3a 2 b + 3ab 2 + b 3 。在第二个例子中,发生了同样的事情,但符号发生了变化。
二项式立方的示例
求解显着恒等式 (x + 3) 3 :
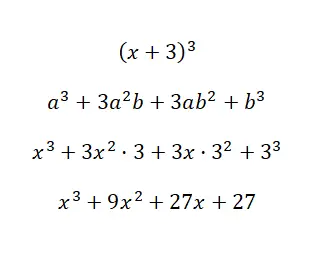
使用我们刚刚讨论的公式,我们可以计算多项式,考虑到:a = xyb = 3。如您所见,过程非常简单,计算中没有太多复杂性,因为我们有公式。否则,要做这么多乘法将是相当乏味的。
立方和与立方差
我们还有另一种情况,它很容易与前一种情况混淆。虽然两种情况写法不同,但并不等同。相当于立方之和或差的表达式是: a 3 + b 3 ,而在前面的例子中我们谈到: (a + b) 3 。正如您所看到的,表达式的结构存在不可否认的相似性,但实际上,在展开计算时,它们是两种完全不同的情况:
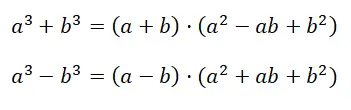
在公式的演示中,我们获得了第一个多项式 的因式分解,准确地说,我们从初始二项式变为二项式与三项式的乘积。看似得到的结果 (a + b) · (a 2 – ab + b 2 ) 并没有简化计算,但实际上,通过对多项式进行因式分解,我们得到了一个非常容易理解的表达式。
立方和的示例
计算显着乘积 x 3 + 27:
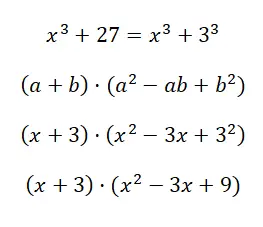
在这种情况下,我们得到的结果相当长,因为它无法进一步简化。但是,得到这个表达式是正常的,事实上,在这些情况下,您只能获得结构相当于二项式与三项式乘积的结果,如本例所示。
三项式的三次方
三项式的立方写为: (a + b + c) 3 ,相当于三个相同的三项式相乘,但没有指数: (a + b + c) · (a + b + c) · (a + b + c).它是最复杂的著名产品,尽管该公式非常合乎逻辑,并且在执行相应的多项式乘法时以与所有公式相同的方式获得。下面您将找到这个非凡恒等式的证明:
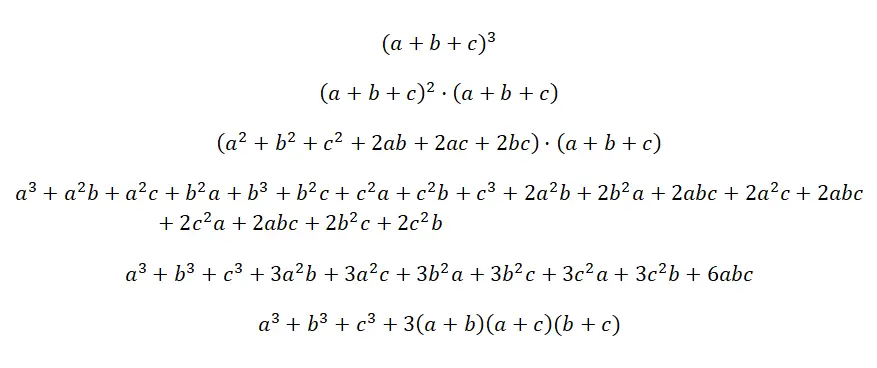
三项式的立方示例
求解以下三项立方 (x 2 + 3x – 4) 3 :
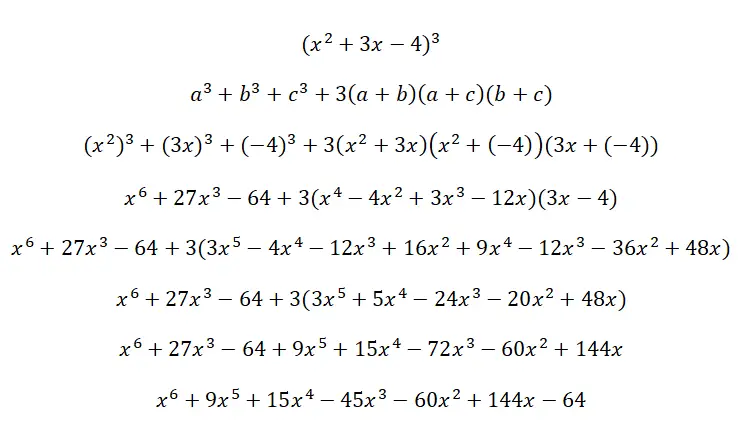
显着的比率
最后,我们将解释显商,它们是快速求解某些类型代数分数的显着恒等式。更准确地说,有四种不同的类型,它们有一个共同的特征:它们的结果由精确的多项式组成(余数为零)。还值得一提的是,卓越商的公式与我们已经解释过的卓越乘积的公式有一定的关系。
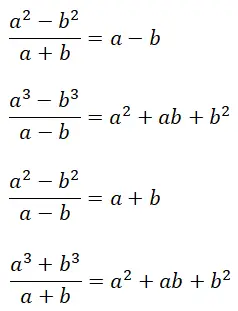
已解决的显着比率示例
计算以下重要比率:
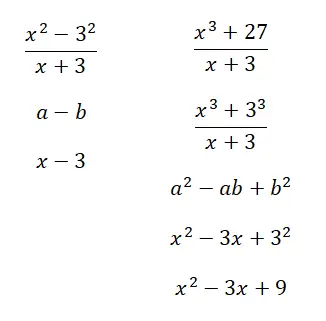
解决了出色的产品练习
现在您已经知道如何解决不同的显着问题,是时候进行一些练习了。这就是为什么我们为您提供6 个练习来应用所解释的所有理论。我们向您展示了主要显着身份的表格,以便您在解决所有练习时可以轻松掌握:

练习1
求解二项式平方 (x – 4) 2 、 (x + 1) 2和 (x – 3) 2 :
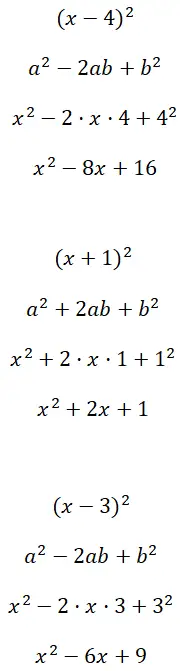
练习2
计算平方 (x – 1) · (x + 1) 和 (x + 3) · (x – 3) 的两个差:
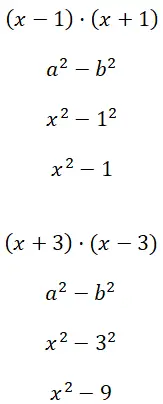
练习3
开发立方 (x – 5) 3和 (x + 8) 3的著名产品:
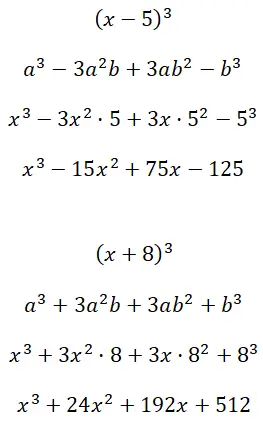
练习4
开发由多因子项 (4x 2 + 5y) 2 、(5x 3 + y 2 ) · (5x 3 – y 2 ) 和 (5xy 2 – 2xy) 2形成的显着恒等式:
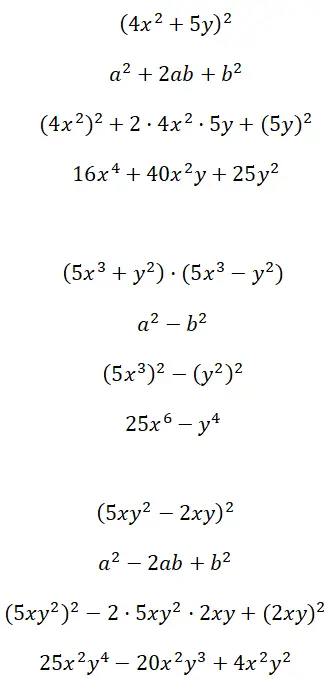
练习5
计算由多因子项 (3x 2 + y) 3和 (5y 3 – 2x 2 ) 3形成的显着三次乘积:
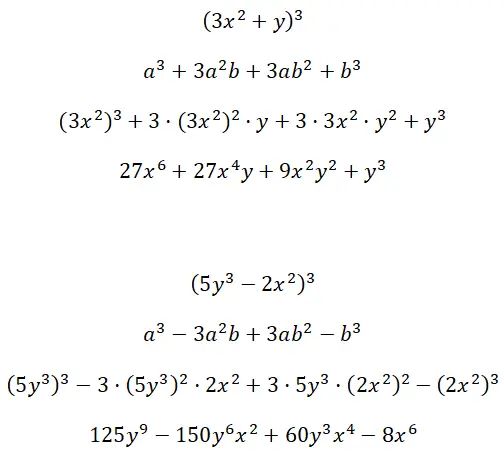
练习6
求解三项式 (2x 2 + 3x + 5) 2和 (3x 2 + 5x + 6) 的平方: