矩阵乘法 - Mathority

在本页中，我们将了解如何对尺寸为 2×2、3×3、4×4 等的矩阵进行乘法。我们通过一个例子一步步解释矩阵乘法的过程，然后你会找到已解决的练习，以便你也可以练习。最后，您将了解两个矩阵何时不能相乘以及该矩阵运算的所有属性。

如何将两个矩阵相乘？

让我们通过一个例子来看看执行两个矩阵相乘的过程：

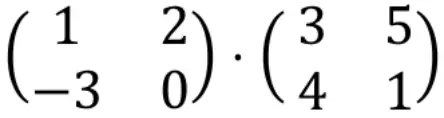
要计算矩阵乘法，左矩阵的行必须乘以右矩阵的列。

所以首先我们需要将第一行乘以第一列。为此，我们将第一行中的每个元素乘以第一列中的每个元素，然后将结果相加。因此，所有这些都将是结果数组第一行的第一个元素。看一下流程：

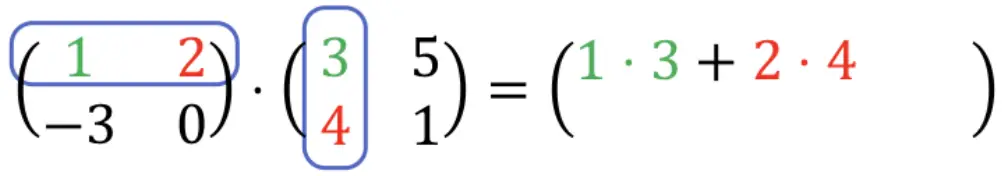
1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11。所以：

现在我们需要将第一行乘以第二列。因此，我们重复该过程：将第一行的每个元素与第二列的每个元素一一相乘，然后将结果相加。所有这些都将是结果数组第一行的第二个元素：

1 × 5 + 2 × 1 = 5 + 2 = 7。所以：

一旦我们填充了结果矩阵的第一行，我们就移动到第二行。因此，我们通过重复以下过程将第二行乘以第一列：将第二行的每个元素乘以第一列的每个元素，然后将结果相加：

-3 × 3 + 0 × 4 = -9 + 0 = -9。然而：

最后，我们将第二行乘以第二列。始终使用相同的过程：我们将第二行的每个元素与第二列的每个元素一一相乘，然后将结果相加：

-3 × 5 + 0 × 1 = -15 + 0 = -15。然而：

到这里两个矩阵的乘法就结束了。正如您所看到的，您需要将行乘以列，始终重复相同的过程：行的每个元素乘以列的每个元素一一相乘，然后将结果相加。

解决矩阵乘法练习

练习1

求解以下矩阵乘积：

查看解决方案

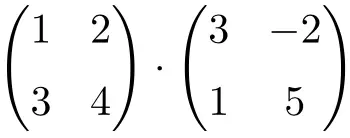
它是 2 阶矩阵的乘积：

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

要求解矩阵乘积，必须将左侧矩阵的行乘以右侧矩阵的列。

所以我们首先将第一行乘以第一列。为此，我们将第一行中的每个元素乘以第一列中的每个元素，然后将结果相加。所有这些都将是结果数组第一行的第一个元素：

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

现在让我们将第一行乘以第二列，以获得结果矩阵第一行的第二个元素：

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

我们转到第二行，因此我们将第二行乘以第一列：

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

最后，我们将第二行乘以第二列，以计算表的最后一个元素：

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

所以矩阵乘法的结果是：

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

练习2

求以下 2×2 方阵乘法的结果：

查看解决方案

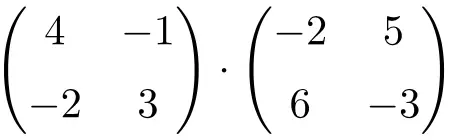
它是 2×2 维矩阵的乘积。

要解决乘法问题，必须将左侧矩阵的行乘以右侧矩阵的列：

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

练习3

计算以下 3×3 矩阵乘法：

查看解决方案

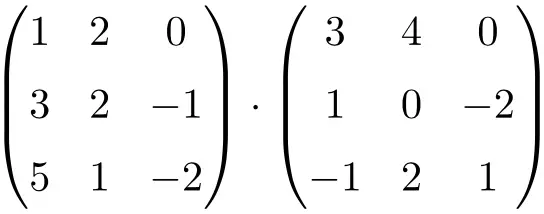
要执行 3×3 矩阵乘法，必须将左侧矩阵的行乘以右侧矩阵的列：

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

练习4

给定矩阵

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

计算：

$\displaystyle 2A\cdot A^t$

查看解决方案

我们首先计算转置矩阵

$A$

做乘法。为了制作转置矩阵，我们需要将行更改为列。也就是说，矩阵的第一行成为矩阵的第一列，矩阵的第二行成为矩阵的第二列。然而：

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

因此，矩阵运算仍然是：

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

现在我们可以进行计算了。我们首先计算

$2A$

（虽然我们也可以先计算

$A \cdot A^t$

）：

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

最后，我们求解矩阵的乘积：

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

练习5

考虑以下矩阵：

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

计算：

$\displaystyle A\cdot B - B \cdot A$

查看解决方案

这是一个将减法与 2 阶矩阵乘法相结合的运算：

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

我们首先计算左边的乘法：

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

现在我们解右边的乘法：

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

最后我们减去矩阵：

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

什么时候不能将两个矩阵相乘？

并非所有矩阵都可以相乘。要将两个矩阵相乘，第一个矩阵中的列数必须与第二个矩阵中的行数匹配。

例如，由于第一个矩阵有 3 列，第二个矩阵有 2 行，因此无法执行以下乘法：

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

但如果我们颠倒顺序，它们就可以成倍增加。因为第一个矩阵有两列，第二个矩阵有两行：

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

矩阵乘法性质

此类矩阵运算具有以下特点：

矩阵乘法是结合的：

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

矩阵乘法还具有分配性质：

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

矩阵的乘积不可交换：

$\displaystyle A \cdot B \neq B \cdot A$

例如，以下矩阵乘法给出结果：

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

但如果我们颠倒矩阵相乘的顺序，乘积的结果会有所不同：

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

此外，任何矩阵乘以单位矩阵都会得到相同的矩阵。这称为乘法恒等性质：

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

例如：

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

最后，正如您可能已经猜到的那样，任何矩阵乘以零矩阵都等于零矩阵。这称为零的乘法性质：

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

例如：

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

如何将两个矩阵相乘？

解决矩阵乘法练习

练习1

练习2

练习3

练习4

练习5

什么时候不能将两个矩阵相乘？

矩阵乘法性质

发表评论 取消回复

发表评论取消回复