在此页面上您将找到零矩阵(也称为空矩阵)的解释。你还会通过例子看到它的元素的值与矩阵的维数无关,最后你会发现该类型矩阵的所有属性。
什么是零矩阵?
零矩阵(或零矩阵)是其元素全部等于零 (0) 的矩阵。
因此,根据零矩阵的定义,该矩阵可以是所有可能的维度,只要它的所有数字都为零。看下面的例子:
空矩阵的示例
2 × 2 零矩阵示例
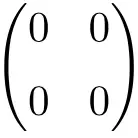
3 × 3 零矩阵示例
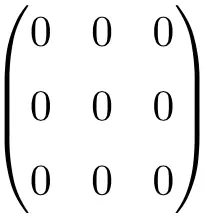
4 × 4 零矩阵示例
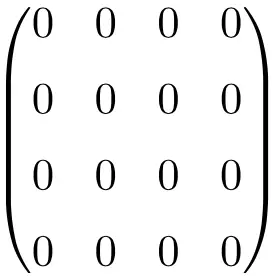
现在您可能认为这个非常特殊的矩阵并不重要,因为它只是一个充满零的矩阵。然而,在数学中,更具体地说在线性代数领域,它是一个非常有用的矩阵,因为它使计算变得更加容易。
零矩阵的性质
空(或空)矩阵具有以下特征:
- 零矩阵是矩阵加法运算的中性元素,因此:
![]()
- 矩阵乘法具有零乘性,即任何矩阵与零矩阵相乘的乘积都等于0。
![]()
- 如果矩阵是方阵,则零矩阵既是对称矩阵又是反对称矩阵。
- 零矩阵是唯一一个秩为零的矩阵。
- 零矩阵的行列式始终为 0,因此这种类型的矩阵没有逆矩阵(它是奇异矩阵)。
- 显然,零矩阵是幂零矩阵的一个例子。