零之间的零不确定性 (0/0)

在本文中，我们将解释当不确定性为 0/0 时如何保存函数的极限。此外，您还可以通过已解决的练习来练习零与零之间的不确定性。

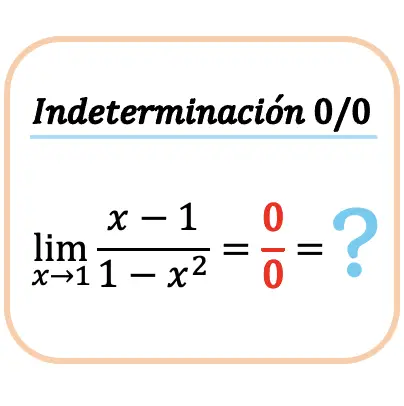
如何解决零（0/0）之间的零不确定性

然后，我们将了解当函数给出零 (0/0) 之间的零不确定性时，如何计算函数的极限。为此，我们将逐步计算一个示例：

我们首先尝试通过将 x 的值代入函数来计算极限：

但我们得到不确定性 0 除以 0。

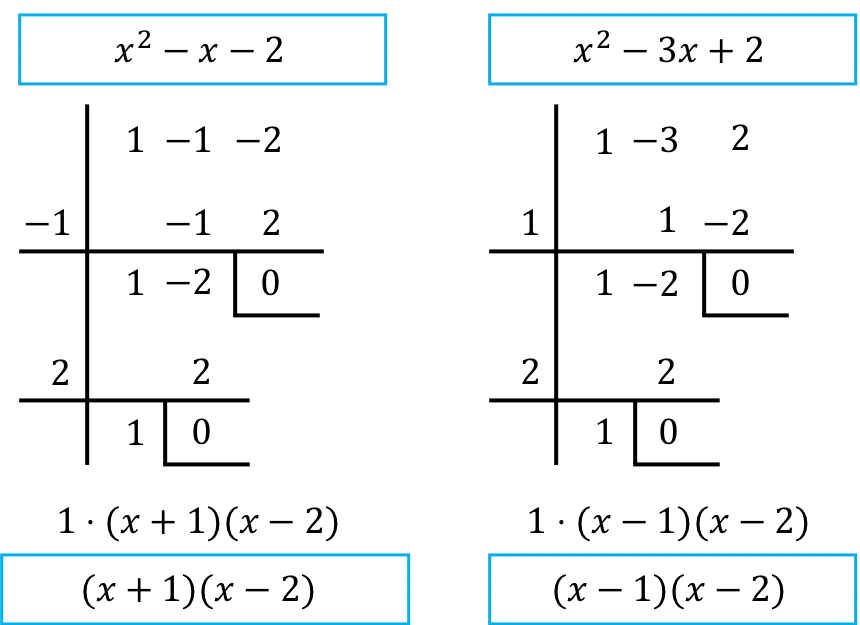
因此，我们必须对分数的分子和分母的多项式进行因式分解。为此，我们使用鲁菲尼规则：

➤如果您不知道如何分解多项式，我们建议您查看我们专门研究多项式的网站上的说明： www.polinomios.org

因此，一旦对多项式进行因式分解，极限如下：

现在，我们可以通过消除分数分子和分母中重复的因子来简化极限：

最后，我们重新计算极限：

正如你所看到的，一旦我们对多项式进行因式分解和化简，就很容易找到极限解。

不确定性 0/0 有根

我们刚刚看到了有理函数的 0/0 不确定性是如何解决的。然而，如果极限是无理（或根式）函数，则 0/0 不确定性的解析方式不同。

首先，我们尝试通过执行以下操作来解决该限制：

但我们的不确定性为零。

➤ 请记住，共轭是相同的无理表达式，但修改了中间符号。

接下来，我们将分数的分子和分母都乘以根式表达式的共轭：

在这种类型的限制内，通过执行此步骤，我们将始终获得可以简化的显着身份。在这种情况下，分母中我们有和与差的乘积，因此：

我们简化分子和分母中重复的因子：

这样我们就可以求出极限的结果：

已解决不确定性练习 0/0

下面我们准备了几个关于给出 0/0 不确定性的函数极限的逐步解决练习。您可以尝试执行这些操作，然后检查解决方案。

不要忘记，您可以在评论中向我们询问有关解决限制的任何问题！

练习1

计算以下有理函数在点 x=-2 处的极限。

从逻辑上讲，我们首先尝试解决极限：

但我们最终得到 0/0 不确定性。因此，我们必须对分子和分母的多项式进行因式分解：

现在我们通过删除分子和分母中重复的括号来简化分数：

最后，我们用简化分数重新计算极限：

练习2

当 x 接近 -1 时，求解以下函数的极限：

我们首先像往常一样尝试解决限制：

但我们得到 0 之间的不确定性 0。因此，我们必须对分数的 2 个多项式进行因式分解：

我们现在可以简化多项式：

我们解决极限：

练习3

确定下列根式函数极限的解：

首先，我们检查极限是否给出某种不确定性：

极限给出了不确定性零除以零，我们在函数中有一个根。因此，我们必须将分数的分子和分母乘以根式表达式的共轭：

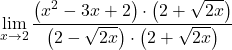
分母对应于和与差的乘积的显着恒等式的发展，因此我们可以简化它：

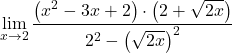
然而，我们还不能简化分数项。因此我们必须对多项式进行因式分解：

这样我们就可以简化分数：

现在我们可以确定极限的结果：

练习4

计算以下根式函数的 x 接近 0 时的极限：

首先，我们像往常一样尝试计算函数的极限：

但我们得到了 0/0 的不确定形式。因此，我们将函数的分子和分母乘以无理表达式的共轭：

我们应用相应的著名恒等公式来简化分母：

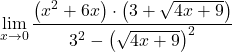
现在我们通过取公因子来对分子的二项式进行因式分解：

我们简化函数分子和分母中重复的因子：

最后，我们解决了函数的极限：

练习5

使用 0/0 不确定性方法求解以下极限：

➤请参阅：如何计算函数的横向极限

我们首先尝试解决限制：

但在极限情况下，我们获得了零对零的不确定性。因此，我们对分子和分母的多项式进行因式分解：

现在我们通过消除分子和分母中重复的因子来简化分数：

我们再次计算极限：

但现在我们发现数字除以 0 是不确定的。因此，我们必须计算当 x 趋于 -1 时函数的横向极限。

我们首先求解函数在左侧点 x=-1 处的横向极限：

然后我们计算函数在右侧 x=-1 处的横向极限：

因此，由于两个横向极限不重合，因此函数在 x=-1 处的极限不存在：