相对于另一个点、直线和平面点对称

在这里，您将了解如何计算相对于另一个点、相对于直线和相对于平面的对称点。此外，您将能够看到逐步解决的示例和练习。

点与另一点对称

在我们了解如何计算对称点之前，我们先回顾一下对称点相对于另一个点到底是什么：

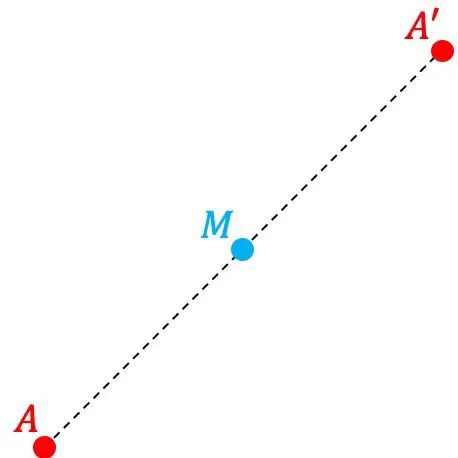
如果点 A’ 对称地位于与点 M 的距离与点 A 和 M 之间的距离相同的位置，则点 A’ 是点 A 相对于另一点 M 的对称点。因此，M 是由下式形成的线段的中点点 A 和 A’。

另一方面，我们也称M点为对称中心。

因此，为了计算对称点的坐标，我们将使用线段中点的公式：

从这个方程中，我们提取未知点 A’，并得到相对于另一个点对称的点的公式：

查找相对于另一点对称的点的示例

作为示例，我们将计算 A 点相对于 M 点的对称点。考虑以下两点：

为了确定这两点之间的对称点，我们应用相对于另一个点的对称点的公式：

现在我们将公式中的点替换：

我们经营：

与直线对称的点

我们刚刚看到了一个点相对于另一个点对称的概念。嗯，点相对于线的对称点非常相似：

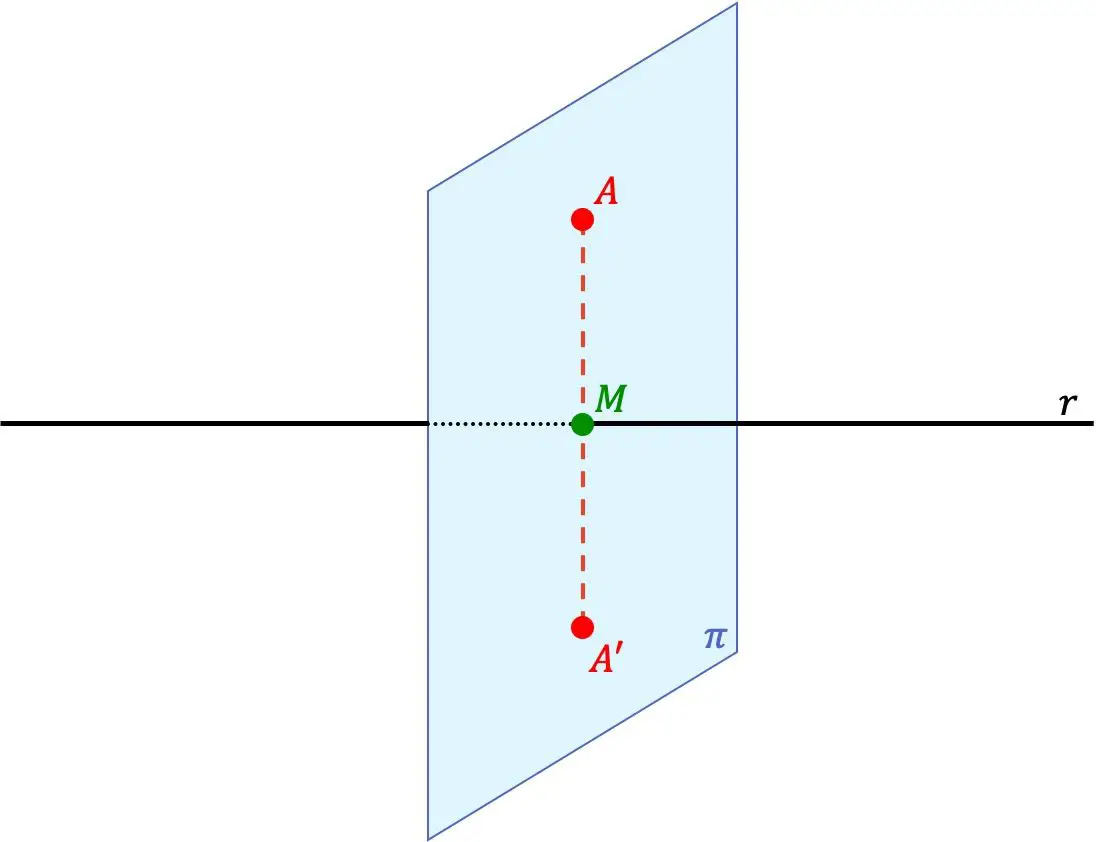
如果两点 A’ 和 A 位于垂直于该直线的同一条直线上，并且点 A’ 与该直线之间的距离等于该距离，则 A’ 点是 A 点相对于直线的对称点A 点与直线之间。

所以直线r也是点之间的对称轴。

因此，要确定 A 点相对于直线r的对称点，我们必须遵循以下过程：

1. 我们找到垂直于穿过点 A 的线r的平面（之前图形表示的平面 π）。为此，我们必须使用直线的方向向量，这将是平面的法线向量。
2. 我们计算找到的平面与直线之间的交点（上图中的 M 点）。
3. 我们使用点对称点公式（见上一节）来找到 A 点相对于 M 点的对称点。结果就是我们要寻找的对称点。

计算直线对称点的示例

一旦我们知道如何计算另一个点相对于一条线的对称点，我们将看到一个解决的练习作为示例：

• 求A点相对于直线r的对称点。正说点和线：

首先，我们需要计算与经过 A 点的直线 r 垂直的平面。垂直于该平面的向量将是直线的方向向量，其分量是参数前面的项

因为它是用参数方程的形式表示的：

且平面方程的系数A、B、C与其法向量的坐标重合，因此：

A 点必须位于该平面上，因此我们现在可以将 A 点代入平面方程中以求出系数 D：

则垂直于穿过A点的直线ry的平面方程为：

一旦我们知道了平面的方程，我们就需要计算平面和直线的交点。为此，我们将直线的坐标代入平面的方程并求解所得方程：

现在我们将值替换为

由直线方程得到：

所以直线r与垂直于它的平面的交点是：

最后找到A点相对于M点的对称点即可；为此，我们可以使用本页开头的公式：

与平面点对称

在了解确定另一点相对于平面的对称点的方法之前，我们先看看它的定义是什么：

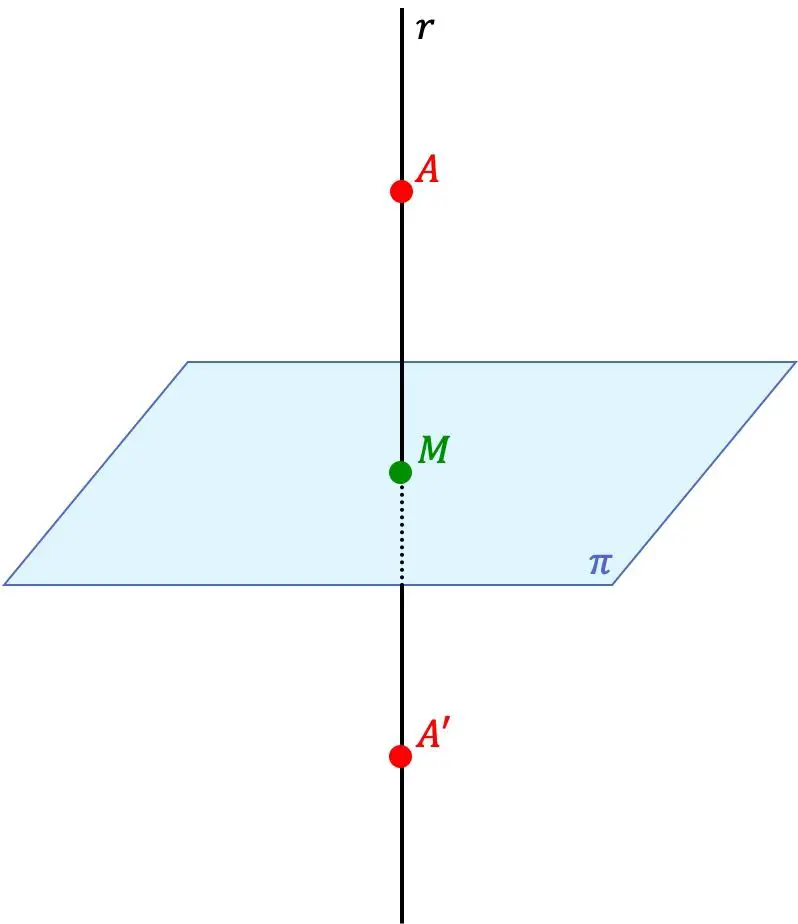
如果两点 A’ 和 A 位于垂直于平面的同一条直线上，且 A’ 点与平面的距离等于A 点与平面之间。

所以该平面也是两点之间的对称平面。

因此，要知道A点相对于平面π的对称点的笛卡尔坐标，必须遵循以下步骤：

1. 我们找到垂直于穿过点 A 的平面的直线方程。为此，我们将使用垂直于平面的向量作为直线的方向向量。
2. 我们计算平面和找到的直线之间的交点（上一张图像的 M 点）。
3. 我们使用关于点的对称点公式（在开始部分中看到）来找到点 A 相对于点 M 的对称点。结果就是我们要寻找的对称点。

确定相对于平面的对称点的示例

下面您可以看到有关另一个点相对于平面的对称点的已解决问题：

• 确定 A 相对于平面 π 的对称点。说了要点和计划：

我们需要做的第一件事是找到穿过 A 点的垂直于平面的直线的方程。为此，我们可以使用垂直于平面的向量作为直线的方向向量，其分量 X， Y、Z 分别是平面方程的 A、B、C 项的系数：

现在我们可以用找到的方向向量及其点之一（A点）来构造与平面正交的直线的参数方程：

一旦我们知道了垂线，我们就可以通过将线的坐标代入平面方程来计算平面和线的交点：

现在我们将值替换为

由直线方程得到：

所以平面与垂线的交点为：

最后，我们只需要找到 A 点相对于 M 点的对称点。为此，我们可以使用本页开头的公式：