▷ 如何知道函数是否连续（已解决的练习）

在本文中，我们将解释什么是连续函数以及如何确定函数在一点处是否连续。此外，您还将发现连续函数的属性以及最常见函数的连续性分析。最后，您可以通过连续函数的已解决练习进行练习，以充分理解该概念。

什么是连续函数？

函数的连续性可以用图形来研究。连续函数是无需从纸上取下铅笔即可在图形上表示的函数。

连续功能

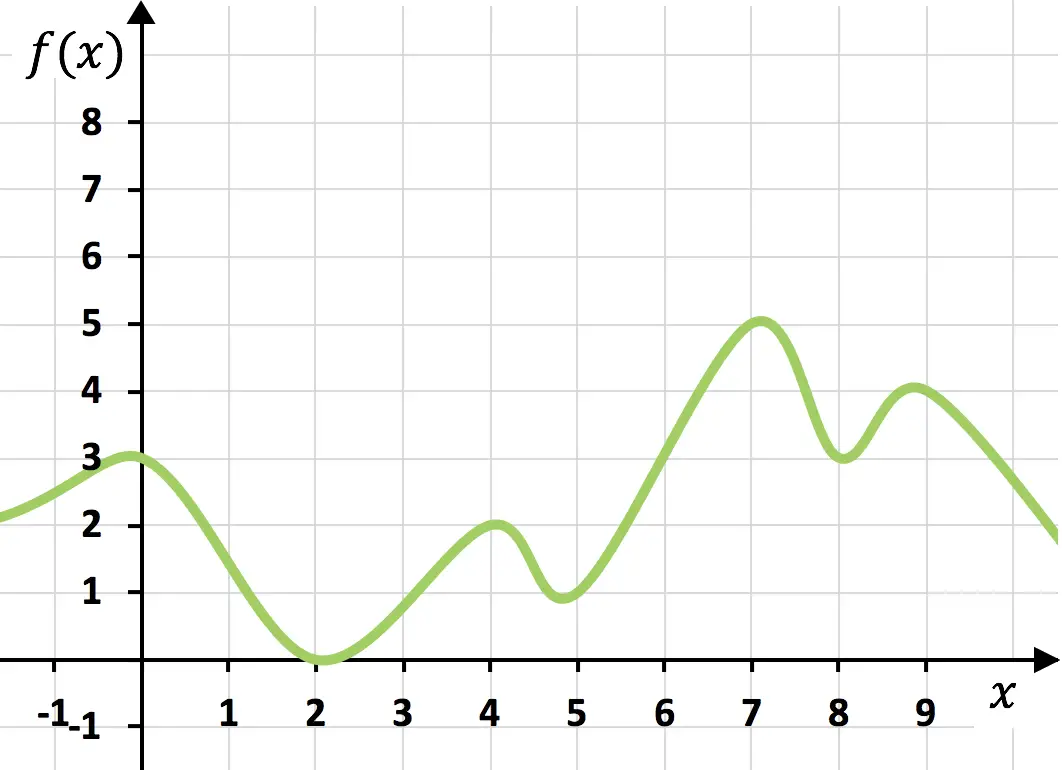
上述功能是连续的，因为它可以一笔画出来，而无需将手从纸上移开。

另一方面，当先前的连续性条件没有放入函数中时，则称该函数为不连续函数。

间断函数

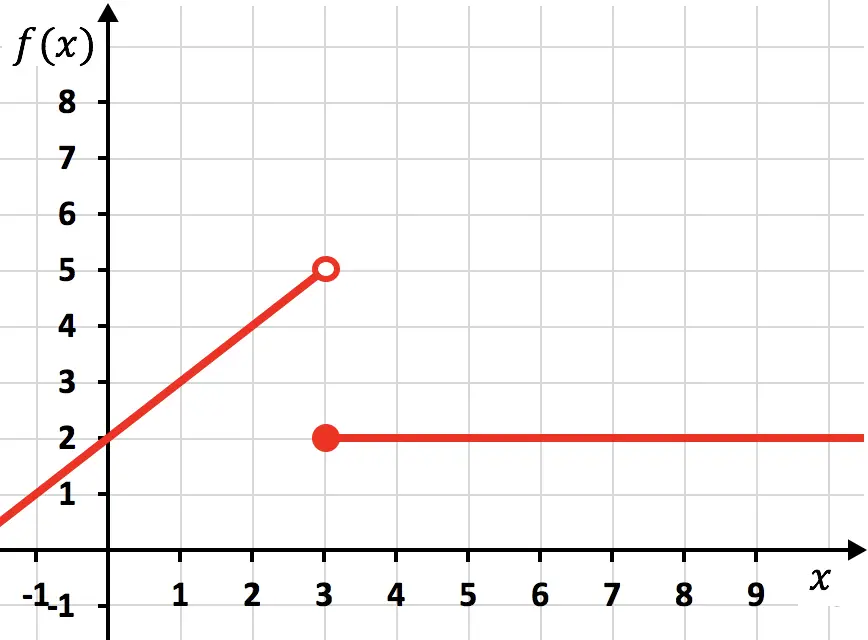
前一个函数是不连续的，因为要表示它，您必须用铅笔画两条线。在这种情况下，函数在 x=3 处不再连续，因此我们说 x=3 是不连续点。

此外，不连续性还分为三种类型：可避免的不连续性、不可避免的有限跳跃不连续性和不可避免的无限跳跃不连续性。在以下链接中，您可以了解每种类型的不连续性的外观以及每种不连续性的不同之处：

➤请参阅：不连续性的类型

函数在一点的连续性

一旦我们看到连续函数的图形是什么样子，我们就会看看如何通过解析来判断函数是否连续。

数学上，如果满足以下三个条件，函数在一点连续：

此时函数存在，即该点的图像存在。

$\exists \ f(a)$

此时功能已受到限制。因此，此时函数的左右侧极限相等。

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

该点的图像与函数在该点的极限重合。

$\displaystyle f(a)=\lim_{x \to a} f(x)$

因此，如果函数的所有点都满足三个连续性条件，则该函数是连续的。

作为例子，我们将分析以下分段函数的连续性：

即使你改变了部分，在这一点上

$x=-2$

该函数是连续的，因为该点处函数的横向极限相等并且与该点处函数的值更一致。

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

另一方面，函数在该点不连续

$x=4$

因为两个横向极限不同，因此此时函数的极限不存在：

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

简而言之，由分段定义的函数在所有实数中都是连续的，除了

$x=4,$

存在不连续性的地方。

我们还可以验证该函数是不连续的

$x=4$

因为要以图形方式表示它，此时必须将铅笔从纸上移开。

初等函数的连续性

某些类型的函数因其特征而连续：

常数函数在所有实数中都是连续的。

$f(x)=k$

多项式函数对于所有实数都是连续的。

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

有理（或分数）函数在所有实数中都是连续的，除了抵消分数分母的值之外，在这些点上函数呈现不连续性。

$f(x)=\cfrac{p(x)}{q(x)}$

指数函数在所有实数上连续：

$f(x)=a^x$

对数函数在使其论证为正的所有点上都是连续的。

$f(x)=\log_a (x)$

无理函数或有根函数的连续性取决于根式 (n) 的指数。如果索引是偶数，则这些在所有点上都是连续函数，使根参数等于或大于零。但如果索引是奇数，则它们是所有实数上的连续函数。

$f(x)=\sqrt[n]{x}$

三角函数的连续性取决于函数的类型。正弦函数和余弦函数在实数集合上连续，但正切函数在点上不连续
$\displaystyle x=\frac{\pi}{2}+k\pi$

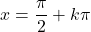
（其中k是整数）。

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

连续函数的性质

肖恩

$f(x)$

和

$g(x)$

两个连续函数在该点

$x=a,$

下一个：

一点上的两个连续函数的和是该点上的另一个连续函数。

$f(x)+g(x)$

两个连续函数在某一点的乘积等于该点的另一个连续函数。

$f(x)\cdot g(x)$

只要该点不取消除法函数，在一点处除以两个连续函数就会在该点得到另一个连续函数。

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

两个连续函数在一点的复合会在同一点产生连续函数。

$f(x)\circ g(x)$

➤请参阅： 什么是复合函数？

解决了函数连续性的练习

练习1

找出下图中所示函数的不连续点。还要确定它是什么类型的不连续性。

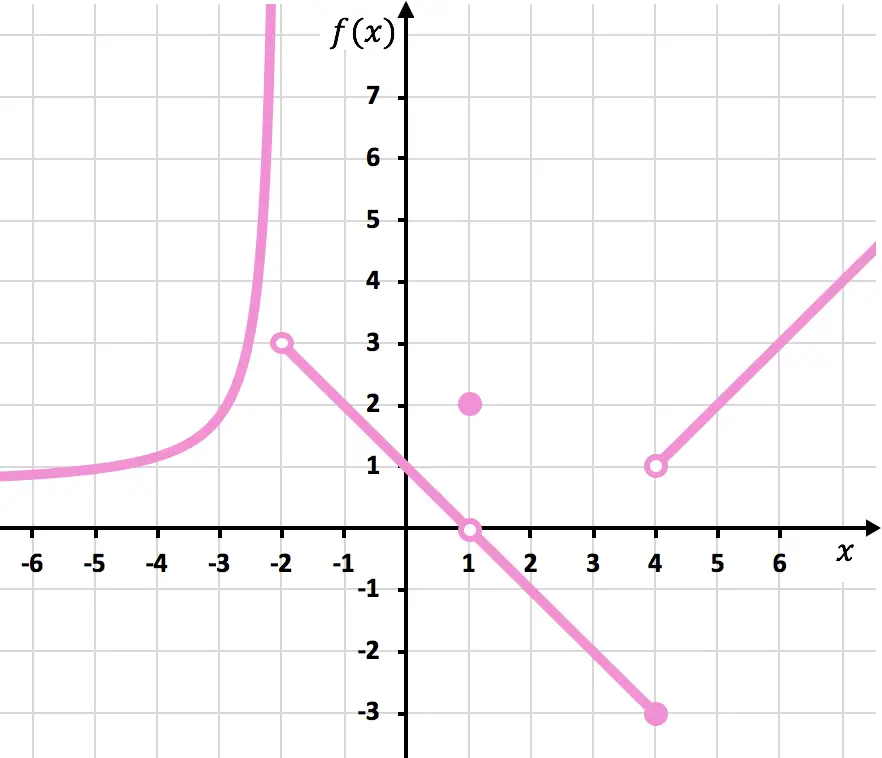
注意：要进行此练习，我们建议您首先了解不同类型的不连续性以及如何识别它们。您可以参阅不连续类型原理链接中的解释。

查看解决方案

要绘制该函数，您必须在 x=-2、x=1 和 x=4 处举起铅笔。因此该函数在这三个点处是不连续的。

在 x=-2 处，左侧极限为 +∞，右侧极限为 3。因此，由于一侧极限为无穷大，因此该函数在 x=-2 处不可避免地存在无限跳跃不连续性。

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

x=1 处函数的极限为 0，另一方面，x=1 处函数的值等于 2。因此，该函数在 x=1 处呈现可避免的不连续性。

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

在 x = 4 时，左侧极限为 -3，右侧极限为 1。因此，由于两侧极限不同且均不给出无穷大，因此该函数在 x = 4 处不可避免地存在有限跳跃不连续性。

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

练习2

确定下图中所示函数不连续的点。

查看解决方案

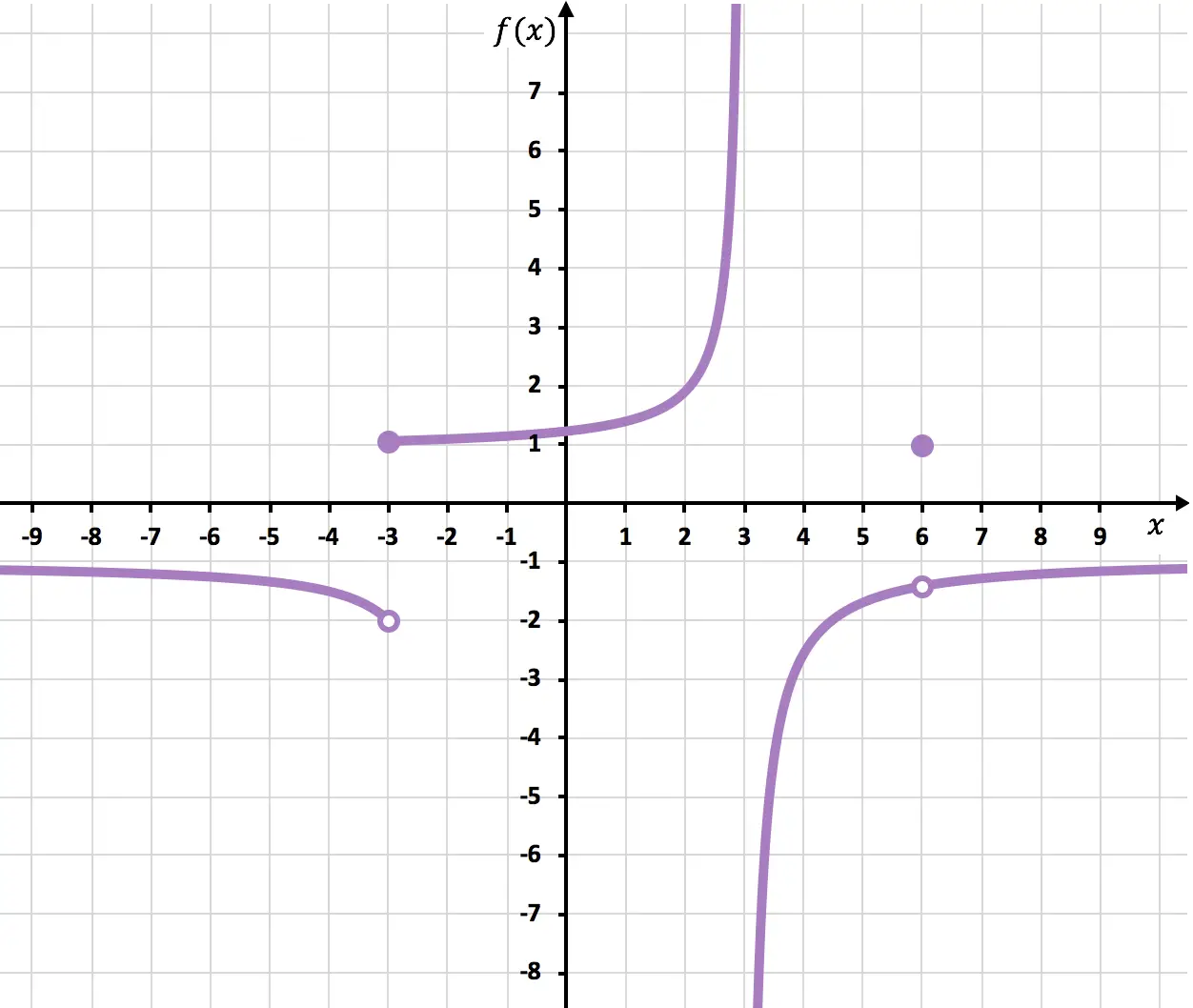
在点 x=6 处，函数因存在开路点而中断。 x 接近 6 时的极限是 -1.4，但 f(6)=1。因此，该函数在 x=6 处具有可避免的不连续性，因为极限值与函数值不一致：

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

当 x=-3 时，横向极限不重合，并且没有给出无穷大。因此，该函数在 x=-3 处具有不可避免的有限跳跃不连续性。

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

最后，该函数在 x = 3 处存在不可避免的无限跳跃不连续性，因为此时至少有一个横向极限会导致无穷大。

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

练习3

分析以下有理函数的连续性：

$\displaystyle f(x)= \frac{2}{x-5}$

查看解决方案

有理函数在其整个域中是连续的，也就是说，在除了抵消分母的值之外的所有实数中。因此，我们将有理函数的分母设置为零，看看哪些点不属于定义域：

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

因此，除了 x=5 之外，该函数在所有点上都是连续的。

练习4

分析以下分段函数的连续性：

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

查看解决方案

该函数在第一部分中也是连续的，

$5x-2$

，如第二部分所示，

$x^2+2$

，因为它们是多项式函数。

因此，函数可能不连续的唯一点是函数分段中断的点。那么我们来计算此时的横向极限：

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

因此两个横向极限重合，当 x 趋于 1 时函数的极限等于 3：

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

此外，x=1的图像也是3：

$f(1)=1^2+2=\bm{3}$

因此，由于函数在 x=1 处的极限等于该点的图像，因此该函数在点 x=1 处连续。因此它在所有实数中都是连续的。

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

练习5

研究以下无理函数的连续性：

$f(x)=\sqrt{2x+6}$

查看解决方案

它是一个偶数下标的根式函数，因此只要根式的自变量大于 0，该函数就是连续的（因为负数的平方根不存在）：

$2x+6\ge 0$

我们解决不等式：

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

解由所有大于或等于-3 的数字组成。因此，该函数在其定义域的区间上是连续的：

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

练习6

分析以下对数函数的连续性：

$f(x)=\log_3 (-3x+6)$

查看解决方案

这是一个对数函数，既没有负数的对数，也没有0的对数。因此，只要对数的参数为正（大于零），该函数就存在：

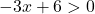$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ 我们解决不等式：

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

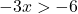
请记住，当您将负数除以不等式的另一边时，必须反转不等式的符号。

$x<2$

该解由所有小于 2 的数字组成。因此，该函数的定义域为：

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

因此，该函数在其域内的每个点都是连续的。

练习7

计算以下函数的连续性：

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

查看解决方案

在分数的分母中，我们有一个具有偶数索引的根式，因此只要根的内容等于或大于零，该函数就会存在：

$-2x-8\geq 0$

而且，根在分数的分母中，而分数的分母永远不可能为 0。因此，只有当根的内容严格大于 0 时，该函数才会存在：

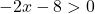$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ 现在我们解决不等式：

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

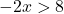
请记住，当我们通过乘或除不等式来改变负数的两边时，我们还必须旋转不等号。

$x<-4$

结果是所有小于-4 的数字。因此，函数的域及其连续性由以下区间定义：

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

练习8

计算k的值，使函数始终连续

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$