在本页中，您将了解 2×2 矩阵的行列式是什么。此外，您还将找到有关如何求解 2 阶行列式的分步解决示例和练习，以便您可以完美地练习和理解它。
什么是2×2行列式？
2 阶行列式是维度为 2 × 2 的矩阵，由矩阵两侧的竖线表示。例如，如果我们有以下矩阵：
![\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50ff006696d04e4eee005e245ba217e4_l3.png "Rendered by QuickLaTeX.com")
矩阵A的行列式表示如下：
![\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc95ca8f173419691852fd137d67154_l3.png "Rendered by QuickLaTeX.com")
正如您所看到的，编写 2×2 方阵的行列式很容易。现在我们看看它是如何计算的：
如何求解2阶行列式？
要计算 2×2 矩阵的行列式，我们需要将主对角线的元素相乘并减去次对角线的乘积。
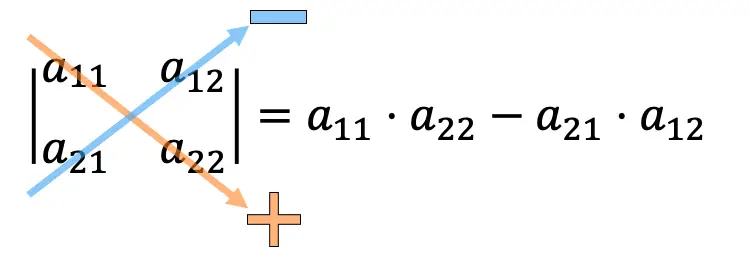
计算 2×2 行列式的示例：
![\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-228cbdabc4e6d330b56fae20f5163e64_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e9aed81d00e74873a5e797746861a51_l3.png "Rendered by QuickLaTeX.com")
解决了 2 × 2 矩阵行列式的问题
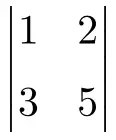
练习1
计算以下 2×2 行列式：
查看解决方案
要生成 2×2 行列式，必须将主对角线的元素相乘并减去次对角线的乘积：
![\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d03764083647c0b05f9a5d7266c8915_l3.png "Rendered by QuickLaTeX.com")
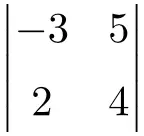
练习2
求解以下 2×2 维行列式：
查看解决方案
要找到 2 阶行列式的解，必须将主对角线的元素相乘并减去次对角线的乘积：
![\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56c917d70b8c6ec3697612d44f84e522_l3.png "Rendered by QuickLaTeX.com")
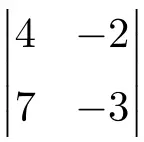
练习3
求以下 2 阶行列式的解：
查看解决方案
要找到 2 维行列式的解，必须将主对角线的元素相乘并减去次对角线的乘积：
![\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cbd06fd83283d3e82105c24eaf95af9f_l3.png "Rendered by QuickLaTeX.com")
练习4
计算以下 2×2 行列式：
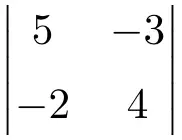
查看解决方案
要计算 2×2 矩阵的行列式，我们需要将主对角线的元素相乘并减去次对角线的乘积：
![\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34915d9aff298587a13346c6fc30bfcd_l3.png "Rendered by QuickLaTeX.com")
练习5
确定以下 2×2 行列式的结果：
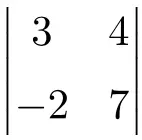
查看解决方案
为了找到 2×2 行列式的解，我们需要将主对角线的元素相乘并减去次对角线的乘积：
![\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c6e4a7fdc04f0458d95c1d62b12d7ac_l3.png "Rendered by QuickLaTeX.com")
明亮的！您现在知道如何创建 2×2 维的行列式了！现在你肯定已经能够理解3×3的行列式是如何计算的，以及4×4矩阵的行列式是如何求解的。