在本节中,我们将了解行列式的所有属性是什么。我们还通过示例演示了每个属性,以便您完全理解它们。此外,您还会找到与限定词属性相关的练习。
下面我们将一一解释行列式的每个属性,但如果您愿意,可以直接跳到下面的汇总表。 😉
性质1:转置矩阵的行列式
矩阵的行列式等价于其转置矩阵的行列式。
![]()
例子:
![Rendered by QuickLaTeX.com \lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e39b73d52e436c660c2c9f2eeed39f6_l3.png)
现在我们转置 2×2 矩阵并求解行列式。请注意,我们获得了与之前相同的结果:
![Rendered by QuickLaTeX.com \lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc16abe425fb139cb3a6b7ba7e3b1915_l3.png)
性质 2:行列式或行列用零填充的行列式
如果行列式的行或列填满了零,则行列式返回 0。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-54df933d2167697d926c25dd9554d90a_l3.png)
例子:
![Rendered by QuickLaTeX.com \begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95bc2d762871764f41176acc052a633c_l3.png)
在这两个示例中,行列式的计算结果均为 0。因为第一个行列式的第二行全为零,第二个行列式的第三列也全零。
性质3:具有两个相等的行或列的行列式
如果行列式具有两个相等或多行或两列,则行列式为零 (0)。
因此,如果行或列之间存在线性组合,即它们是线性相关的,则行列式给出0。
例子:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c31b59570d4f89e8c7e7aa9f922977c5_l3.png)
在本例中,行列式给出 0,因为第 2 列和第 3 列相等。
属性4:修改行列式的行或列
如果两行或两列相对于彼此修改,则行列式给出相同的结果但具有不同的符号。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-de79fc53e94c9a30d8a271d42d4e3494_l3.png)
例子:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2e4806318fa67998b339383a9dc9ea5_l3.png)
现在我们更改第 2 列和第 3 列相对于彼此的顺序。请注意,结果相同但符号不同:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a4de8b8cf37df2c3cce69d16a19a578_l3.png)
性质 5:行列式乘以标量
将整行或整列中的所有元素乘以实数与将行列式的结果乘以该数相同。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06cf5f62a3d703b43bb68b319839df26_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7b38fe06dab0bbdbfef384b3e403fed_l3.png)
例子:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92b404bb7ad8bbdd59c8c54c1619c37d_l3.png)
现在我们采用相同的行列式并将整行乘以 2。您将看到结果将是前一个行列式的结果,但乘以 2 或 10:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57ae1ba33c0d108f08ac9d0b5cb4a81b_l3.png)
性质 6:矩阵乘积的行列式
两个矩阵的乘积的行列式分别等于每个矩阵的行列式的乘积。
![]()
例子:
为了证明行列式的这一性质,我们将以两种可能的方式计算以下两个矩阵相乘的行列式:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38de0ca99ad15f40bd94f653cffacf8d_l3.png)
我们首先将两个矩阵相乘,然后计算所得矩阵的行列式:
![Rendered by QuickLaTeX.com \displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2ad18d1637b581038b7866030d6ac9a0_l3.png)
现在我们分别计算每个矩阵的行列式,然后将结果相乘:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f7c97d5a832d3985bf1d5e9d4d44401_l3.png)
正如您所看到的,先计算矩阵乘积,然后计算行列式,与先计算每个矩阵的行列式,然后将结果相乘得到的结果相同。
另一方面,这个条件不适用于加法和减法运算,也就是说,两个矩阵的行列式相加(或相减)的结果与两个矩阵的行列式相加(或相减)的结果不同。分别是两个矩阵。
性质7:逆矩阵的行列式
如果一个矩阵是可逆的,那么它的逆矩阵的行列式就对应于原矩阵的行列式的逆矩阵。
![]()
例子:
我们将通过首先计算矩阵的逆,然后求解其行列式来验证此属性。我们会看到结果相当于找到原始矩阵的行列式并将其求逆。
因此,我们反转以下矩阵并计算其行列式:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c77c10006d35ebc5273553fb84356e3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a9315a8add365cd5f077c52476a827d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a10c873ff6c101cd2b239388393c268b_l3.png)
现在我们求解原始矩阵的行列式并求其逆:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-850e5404f5352782327918caab3e1440_l3.png)
![]()
正如您所看到的,两个操作的结果是相同的。因此该性质得到证明。
性质8:替换限定符的行
行列式的行可以通过添加(或减去)同一行加上(或减去)另一行乘以一个数字来替换。
例子:
通过以下示例,我们将检查此属性。我们首先计算一个行列式,然后对行列式的一行进行操作并重新计算其结果。您将看到我们如何在这两种情况下获得相同的结果。
因此,我们首先用 Sarrus 规则计算 3×3 行列式:
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ccd76fc3a2b7cd7afc7d8f9de8ffde1_l3.png)
现在,在第 2 行中,我们将第一行乘以 2:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4bc2e6bd78446fb68f29b4a5503a6828_l3.png)
我们在变换行列式之一后求解行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-045eb6f32420fbbf538a9e0a540ce119_l3.png)
两种情况的结果都是-3。因此,表明如果一行被替换为同一行加上另一行乘以一个数字的总和,则行列式的结果不会改变。
性质9:三角矩阵的行列式
三角矩阵的行列式是其主对角线元素的乘积。
例子:
我们以求解以下三角矩阵的行列式为例:
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}](https://mathority.org/wp-content/ql-cache/quicklatex.com-40ebfa5f9f06e63ad1325d9331a57bde_l3.png)
性质10:对角矩阵的行列式
对角矩阵的行列式等于其主对角线元素的乘积。
例子:
让我们以以下对角矩阵的行列式为例:
![Rendered by QuickLaTeX.com \begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56e1b3093685a1af729310752b03dfc9_l3.png)
行列式性质汇总表
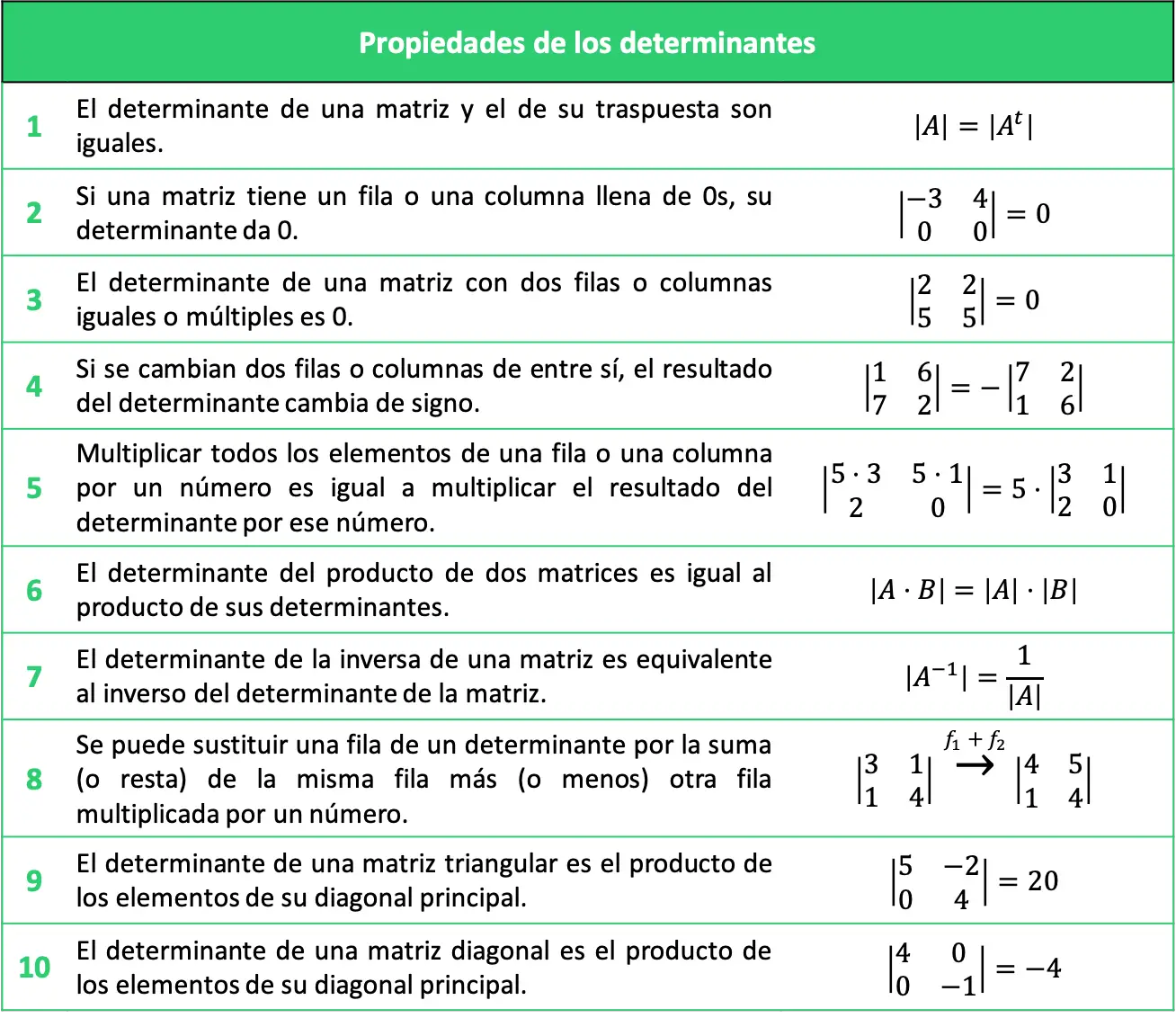
所解释的行列式的属性可以总结在下表中:
解决具有行列式性质的练习
练习1
求解下列行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97dfc1ebfc5db73750870911108bd447_l3.png)
如果行列式的行或列填满了零,则行列式返回 0(属性 2)。因此,行列式的结果是0,因为第三列被零填充。
练习2
求解下列行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdb315ba588fe5fdfb03c7fea2857b16_l3.png)
如果行列式具有两个相等或多行或两列,则行列式返回 0(属性 3)。因此,行列式的结果是0,因为第一行和第三行相等。
练习3
计算以下行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96c5cfee4c4189e49b54fdf43b2a0457_l3.png)
如果行列式具有两个相等或多行或两列,则行列式返回 0(属性 3)。因此,行列式的结果是0,因为第四列是第一列的两倍。
练习4
尽管我们不知道矩阵的元素,但我们知道行列式的结果:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-e20d9016edd52f18d3ffc928d2658efe_l3.png)
根据前一个行列式的结果和行列式的性质,计算以下行列式的结果:
![Rendered by QuickLaTeX.com \displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c20de8d82171dc8fb784e2549521f37_l3.png)
为了)
![]()
是的转置矩阵
![]()
。并且矩阵的行列式等于其转置矩阵的行列式(性质1)。因此,该行列式的结果也是3。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bf7ae0a2ff32d75a6f7abafb623639c_l3.png)
b)在确定
![]()
第 1 列和第 2 列已针对语句的限定符进行了修改
![]()
。因此,根据性质4,结果与该语句的判定符的结果相同,但符号不同,即-3。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6d14aa2f6b8c7d1fd064daef8dd0eec_l3.png)
c)在确定
![]()
该语句的行列式的整个第二列都被乘以了3。因此,从属性5我们可以推断出它的结果也将是该语句的行列式乘以3的结果,即9。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1a7ffec429367a2fd967a197d0299d2_l3.png)
练习5
我们知道这两个决定因素的结果:
![Rendered by QuickLaTeX.com \displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8](https://mathority.org/wp-content/ql-cache/quicklatex.com-e938c40ce401263da9835fa77fc9a1dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4](https://mathority.org/wp-content/ql-cache/quicklatex.com-6cea0d73e66099f2a10f71f7267baee9_l3.png)
根据该信息,计算:
![]()
要计算行列式的结果,不需要将 4×4 矩阵相乘。由于两个矩阵的乘积的行列式分别等于每个矩阵的行列式的乘积(性质6)。然而:
![]()