绝对误差和相对误差是用于评估计算或估计精度的两种度量。
绝对误差是指实际值与估计值之间的差异。就其本身而言,相对误差是指绝对误差与真实值之间的比率。
两者都很重要,因为它们提供了有关结果的准确性和相关性的信息。此外,它们广泛应用于许多领域,包括工程、物理和经济学。我们在下面逐一进行描述。
绝对误差是多少?
绝对误差是测量值或估计值与实际值之间差异的度量。
用公式表示: |测量值-真实值| 。换句话说,绝对误差是测量值或估计值与实际值之差的绝对值。
用数学语言表达的话,则为:
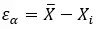
值得一提的是,它是科学、技术、工程和经济等许多领域的基本衡量标准,因为它可以评估结果的准确性以及模型和估计的质量。
绝对误差是如何计算的?
计算绝对误差很简单:
从实际值中减去测量值或估计值,并取结果的绝对值。
例如,如果实际值为 10,测量值或估计值为 9,则绝对误差为:
|9 – 10| =|-1| = 1。
另一个例子,如果实际值为 15,测量或估计值为 17,则绝对误差为:
|17 – 15| =|2| = 2。
您还可以计算平均绝对误差,它是绝对误差的总和除以测量或估计的数量。要计算它,您必须遵循以下公式:
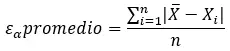
当您有许多测量或估计并且想要大致了解结果的准确性时,这非常有用。
假设我们有以下测量或估计:
当前值:20
测量值1:18
测量值2:22
测量值3:19
我们计算每次测量的绝对误差如下:
绝对误差1:|18 – 20| = 2
绝对误差2:|22 – 20| = 2
绝对误差3:|19 – 20| = 1
我们计算平均绝对误差如下:(2 + 2 + 1) ÷ 3 = 1.67。这表明平均而言,测量值或估计值与真实值的偏差在 1.67 个单位以内。
相对误差是多少?
相对误差是用绝对误差与真值之比来衡量测量或估计的精度。
用公式表示:(绝对误差)÷(实际值) 。用数学语言表达的话,则为:
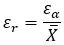
相对误差对于比较不同测量或估计的精度很有用,特别是当实际值不同时。
相对误差是如何计算的?
在计算相对误差时,将对绝对误差进行归一化,以便可以独立于实际值来比较不同测量或估计的精度。
例如,假设您有两个测量值或估计值 A 和 B,其真实值分别为 10 和 100,绝对误差分别为 1 和 5。
测量 A 的相对误差为 (1) ÷ (10) = (0.1),而测量 B 的相对误差为 (5) ÷ (100) = (0.05)。这表明测量 B 相对而言比测量 A 更准确,尽管它具有更大的绝对误差。
以下是如何计算相对误差的一些示例:
1.测量建筑物的高度,估计为100米:
经过测量,我们发现它实际上有98米长。
绝对误差为 2 米,相对误差为 (2) ÷ (98) = 0.0204 或 2.04%。
2. 假设您要测量一个物体的重量,并且您估计该物体的重量为 10 公斤。
经过测量,我们发现它的实际重量为9.5公斤。
绝对误差为 0.5 千克,相对误差为 (0.5) ÷ (9.5) = 0.0526 或 5.26%。
3. 假设您要测量一块木板的长度,估计为 200 厘米。
测量后发现,实际是201厘米。
绝对误差为 1 厘米,相对误差为 (1) ÷ (201) = 0.00498 或 0.498%。
在每个示例中,相对误差以绝对误差与真实值的比率来衡量测量精度。这使您可以比较不同测量和估计的准确性,无论其实际值如何。
绝对误差和相对误差有什么区别?
绝对误差和相对误差是评估结果或模型准确性的两种不同度量。
绝对误差是指某个量的实际值或真实值与估计值或测量值之间的差异。它可以计算为实际值与估计值之间的差值:
绝对误差=实际值-估计值
绝对误差可以是正值,也可以是负值,具体取决于估计值是大于还是小于真实值。
另一方面,相对误差是指绝对误差与实际值或真值之间的关系。它可以计算为绝对误差与真值的分数:
相对误差=绝对误差÷实际值
相对误差通常用百分比表示。这种类型的误差使得可以比较不同结果或模型的准确性,无论其大小如何。
例如,1.0 的绝对误差可能是少量的显着偏差,但不是大量的偏差。然而,两种情况下的相对误差是相同的。
简而言之,绝对误差衡量实际值与估计值之间的差异,而相对误差则衡量估计值与实际值的关系的准确性。
绝对误差和相对误差有哪些应用?
绝对误差和相对误差在不同领域有着广泛的应用,包括:
- 科学——在科学实验中评估测量的准确性和结果的质量。
- 技术– 用于评估机器和设备精度的制造和质量控制。
- 工程– 用于评估测量精度并确保成品质量的施工和设计。
- 经济学:资产评估和财务风险评估,以评估预测的准确性并做出明智的决策。
- 数学和统计学:建模和估计以评估结果的准确性并改进模型。
绝对误差和相对误差计算示例
以下是计算绝对误差和相对误差的两个简单示例:
1. 假设一个物体的重量估计为 3.0 千克,实际重量为 2.8 千克。
我们计算绝对误差如下:
绝对误差 = 实际值 – 估计值 = 2.8 kg – 3.0 kg = -0.2 kg
我们计算相对误差如下:
相对误差 = 绝对误差 ÷ 实际值 = -0.2 kg ÷ 2.8 kg = -0.0714 或 -7.14%
2. 假设一个容器的容积估计为50升,实际容积为45升。
我们计算绝对误差如下:
绝对误差 = 实际值 – 估计值 = 45 升 – 50 升 = -5 升
我们计算相对误差如下:
相对误差 = 绝对误差 ÷ 实际值 = -5 升 ÷ 45 升 = -0.1111 或 -11.11%
3. 假设一个城市的人口估计为100万人,实际人口为97.5万人。
我们计算绝对误差如下:
绝对误差 = 实际值 – 估计值 = 975,000 – 1,000,000 = -25,000
我们计算相对误差如下:
相对误差 = 绝对误差 ÷ 实际值 = -25,000 ÷ 975,000 = -0.0257 或 -2.57%
4、假设一个足球场的面积估算为10000平方米,实际面积为9900平方米。
我们计算绝对误差如下:
绝对误差=实际值-估算值=9900-10000=-100平方米
我们计算相对误差如下:
相对误差 = 绝对误差 ÷ 实际值 = -100 ÷ 9900 = -0.0101 或 -1.01%
在这些示例中,绝对误差和相对误差告诉我们估计的精度。绝对误差告诉我们估计值与真实值的偏差有多大,而相对误差告诉我们估计值与真实值的关系偏离了多少。