▷ 什么是组合数以及如何计算组合数（示例）

在此页面上，我们解释什么是组合数以及它的计算方式（公式）。此外，您将能够看到如何计算任何组合数的示例，并通过逐步解决的练习进行练习。我们还展示了组合数的所有属性和应用。最后，我们学习如何直接使用计算器求组合数的结果。

什么是组合数？

在数学中，组合数也称为二项式系数，是由 n 个元素（n>k）组成的 k 个元素组的普通组合（不重复的组合）的数量。

组合数在括号中表示如下：

$\begin{pmatrix}n \\ k \end{pmatrix}$

另一方面，组合数是通过k读取的。同样， n称为分子， k称为阶。

仅凭组合数的定义，很难理解其含义。然而，我们现在将了解如何用数学方法确定组合数，然后我们将更深入地研究组合学的概念。你会发现这样你会更好地理解它。

组合数公式

组合数（或二项式系数）值的计算公式如下：

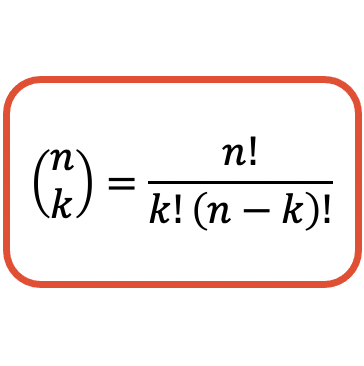
请记住，在代数中，感叹号对应于数字的阶乘。要求一个数的阶乘，您需要将所有 1 的正整数乘以该数。例如，要计算数字 4 的阶乘，您必须将 1、2、3 和 4 相乘：

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

了解 0 的阶乘等于 1 也很重要。

$0! = 1$

计算组合数的示例

接下来，我们将以一步步确定组合数的值为例，让您看看它是如何完成的：

计算组合数 5 除以 3 的值。

5 除 3 的二项式系数对应于以下表达式：

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

因此，如果我们应用组合数的公式，为了确定其值，我们必须执行以下操作：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

或同等学历：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

因此我们找到阶乘：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

乘法 1·2·3 在分子和分母中重复，因此可以通过消除这个因子来简化分数：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

现在我们计算乘积：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

最后，我们进行划分：

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

组合数的性质

组合数或二项式系数可以根据以下属性进行组合：

两个互补组合数是具有相同分子n且其阶数之和等于该分子n的组合数。因此，两个互补组合数的结果是相同的。

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

组合数的这种特性也称为对称性。

例如，6 除 4 的结果与 6 除 2 的结果相同，因为 6-4=2。

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

具有相同分子和顺序的两个组合数的和等于另一个组合数，该组合数的分子等于加法的分子加1，并且其阶对应于加法的阶数中的最大值。换句话说，总是满足以下条件：

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

例如：

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

该性质也称为帕斯卡法则。

另一方面，这个公式也可以反向应用，将一个组合数分解为两个更简单的组合数：

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

例如，组合数 8 除 4 等于 7 除 3 加 7 除 4：

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

任何大于 1 的正数都等于该数本身。

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

该属性的原因是一个数字的阶乘等于前一个数字的阶乘乘以该数字本身：

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

此类组合数的示例：

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

任何大于 0 的正数都等于 1。

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

事实上，这样的组合数的分数的分母将始终等于分数的分子：

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

组合数的例子如下：

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

每个数字本身都等于 1。

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

这是演示：

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

组合数的例子如下：

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

如何用计算器计算组合数

到目前为止，我们已经了解了如何找到或多或少简单数字的组合数，但是当我们必须处理非常大的数量时，最好使用计算器来确定组合数。现在我们将了解如何在计算器中输入组合数字。

因此，用计算器计算组合数的键是nCr 键。而要确定组合数的值，必须先输入组合数的分子，其次按nCr键，然后输入组合数的顺序，最后按等于键。

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

在 CASIO 科学计算器上，nCr 键通常有自己的按钮或位于除法按钮上方，具体取决于型号。

例如，如果我们想知道 10 除以 6 的组合数是多少，我们必须执行以下序列：

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

组合数的应用

如果您已经做到了这一点，您可能已经知道如何解决任何组合数，完美。但是……组合数有什么用呢？好吧，那么我们将看到这种非常特殊的操作所带来的所有优点。

组合学

正如我们在页面顶部看到的，组合数的结果

$\begin{pmatrix}n\\ k \end{pmatrix}$

表示可能的组数

$k$

可以由一组总共构成的元素

$n$

项目。

因此，一些组合问题可以使用组合数（或二项式系数）来解决。让我们通过一个例子来看看如何做到这一点：

在一个 30 名学生的班级中，我们想要选择一组 4 名学生来执行某些任务。总共可以组成多少个不同的组？

在这种情况下，学生的顺序并不重要，同一学生不会在组内重复两次，并且并非所有学生都进入该组。因此，可以利用组合数公式来确定该群可以有多少种形成方式。

为此，您必须以学生总数为分子，以组成小组的学生人数为顺序计算组合数：

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

因此，可能的组合总数为 27,405 组。

牛顿二项式

组合数的另一个应用是牛顿二项式。牛顿二项式是由两项一起求成整数的多项式，也就是说，牛顿二项式是响应以下代数表达式的多项式：

$(a+b)^n$

显然，如果二项式是平方的，则意味着它是显着的恒等式，因此可以很容易地用相应的公式进行计算。另一方面，当二项式增大到很大的数时，计算就变得相当困难。牛顿二项式定理表明，这些类型的多项式可以很容易地从组合数计算出来。

单击以下链接，了解牛顿二项式公式是什么及其计算方法。此外，您将能够看到示例并通过逐步解决的练习进行练习。最后，您将发现这个定理的奇妙历史。

塔塔利亚（或帕斯卡）三角形

正如您在本文中所看到的，手动计算大数的二项式系数可能既费力又复杂。

另一方面，使用塔塔利亚三角形（也称为帕斯卡三角形），可以使用助记符规则轻松确定所有组合数。这在逻辑上非常有用，因为它在计算过程中节省了大量时间。

要确切了解如何执行此操作，请参阅塔尔塔利亚的三角形解释。在此链接页面上，您将了解这个神秘的三角形是什么、它的用途是什么（它有令人惊讶的应用）😮以及它的起源是什么（它已经在 1000 多年前被使用）。

解决了组合数练习

为了让您能够练习并充分理解所解释的概念，我们为您提供了几个逐步解决组合数的练习。

练习1

找出 9 × 5 的组合数（不使用计算器）。

查看解决方案

要找到 5 个组合数中的 9 个的值，我们只需应用阶乘公式：

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

练习2

下面两个组合数相加的结果是什么？（不带计算器）

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

查看解决方案

根据组合数的性质，问题的总和等于以下组合数：

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

因此，计算 7 中的组合数 11 就足够了：

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

练习3

判断下列组合数是否相等：

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

查看解决方案

要找到三个组合数的结果，您不需要使用计算器，但由于组合数的性质，它们可以很容易地找到。

首先，任意大于0的数的组合数都是1。因此：

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

另一方面，任何大于一的数字都等于该数字本身。然而：

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

最后，任何由相同数字重复两次形成的组合数都等于 1。所以：

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

综上所述，问题中的第一个和第三个组合数相等，但与中间的组合数不同。

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$