线性回归是一种用于研究两个连续变量之间关系的统计方法。线性回归的主要思想是找到最适合数据的直线。此外,它还允许您根据一个变量的值来预测另一个变量的值。
这条直线称为“回归”,用于预测未知值或了解变量之间的关系。总之,线性回归是分析和建模两个连续变量之间关系的工具。
为什么线性回归很重要?
线性回归很重要,因为它允许您对两个连续变量之间的关系进行建模和分析,这对于预测未来值和识别数据模式和趋势非常有用。
此外,线性回归是统计学以及大多数科学和社会研究领域的基本工具,包括经济学、心理学、医学、工程和物理学等。它还用于工业和商业中的业务决策和流程优化。
总之,线性回归是一种强大且多功能的工具,可以分析和更好地理解各个研究和实践领域的数据以及变量之间的关系。
线性回归有哪些类型?
线性回归有多种类型,其中一些是:
简单线性回归
简单线性回归分析是一种广泛使用的工具,用于研究自变量对单个因变量的影响,其中认为它们之间存在线性关系。简单的线性回归方程允许我们根据自变量的值来估计因变量的值。
简单线性回归公式为:
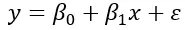
其中,β 0是自变量为零时因变量的值。 β 1表示自变量每单位变化引起的因变量变化,ε 表示残差或误差。即数据的变异性无法用公式的线性关系来解释。
多元线性回归
当存在多个可以影响所研究的因变量的自变量时,使用多元线性回归。
多元线性回归的公式为:
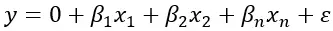
其中Y代表因变量, β 1 、β 2 、β n是影响Y值、回归的自变量,ε代表可能存在的误差。这个公式允许我们根据自变量的值来估计Y的值。
线性回归公式是什么?
线性回归公式为:
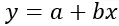
金子:
y 是要预测的因变量(或响应)
x 是用于进行预测的自变量(或预测变量)
a 是截距(或者当 x=0 时回归线与 Y 轴相交的点)
b是回归线的斜率(表示x每次变化时y的变化率)
为了找到 a 和 b 的值,我们使用最小二乘法,该方法旨在最小化观测值与回归线预测值之间的平方误差之和。
以下是公式:
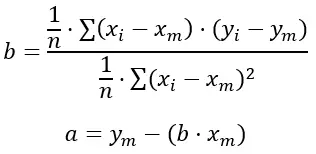
金子:
n 是我们拥有的数据集总数。
x i和y i是我们求和时取的值。
x m和y m是每个变量的平均值。
如何应用线性回归方法?
线性回归方法可以按照以下步骤应用:
- 收集数据:首先要做的是收集您感兴趣的数据。例如,如果你想研究一群人的工资和年龄之间的关系,你需要收集他们每个人的工资和年龄的信息。
- 绘制数据– 接下来,您需要在笛卡尔平面上绘制数据,其中自变量(在本例中为年龄)放置在水平轴上,因变量(工资)放置在垂直轴上。
- 确定回归线:必须确定最适合数据的回归线。这条线是根据线性回归公式获得的,该公式是使用样本统计数据计算得出的。
- 评估拟合优度– 评估回归线与数据的拟合程度非常重要。这可以通过统计测量来完成。
- 进行预测——最后,可以使用生成的回归线进行预测。例如,如果你想预测一个30岁的人的工资,你可以使用线性回归公式并将年龄值代入其中。
值得注意的是,这些步骤可能会略有不同,具体取决于所使用的线性回归类型和所使用的统计软件。
线性回归有什么用?
当您想要分析两个变量之间的关系(其中一个变量可以影响另一个变量的值)时,可以使用线性回归。因此,线性回归可用于了解自变量如何影响因变量,并根据自变量预测因变量的值。
需要注意的是,线性回归假设两个变量之间的关系是线性的,这意味着因变量的变化与自变量的变化成正比。
因此,当怀疑两个变量之间存在线性关系时,应使用线性回归。如果不满足这个条件,使用其他非线性回归模型或不同的统计方法可能更合适。
线性回归有哪些应用?
线性回归在统计学、经济学、工程学、社会科学、生物学等领域有着广泛的应用。以下是线性回归的一些最常见的应用:
- 趋势分析——分析历史数据的趋势并预测未来的趋势。
- 预测——根据一个或多个变量的过去值预测变量的未来值。
- 市场研究:研究产品的需求与其价格之间的关系。
- 财务分析——研究公司收入和支出之间的关系并预测未来的财务结果。
- 流行病学研究:研究暴露于危险因素与患病概率之间的关系。
- 社会科学——研究心理学、社会学和政治学等领域的两个或多个变量之间的关系。
- 运筹学– 线性回归用于对工业工程和物流等领域的复杂系统进行建模和优化。
- 环境科学——用于研究环境因素与生态系统影响之间的关系。
线性回归中的残差是什么?
线性回归中的残差是因变量的观测值与线性回归模型预测值之间的差值。换句话说,它是实际数据点与回归线之间的垂直距离。
残差背后的想法是,如果回归线很好地拟合数据,则残差应该很小且随机。如果残差很大或遵循某种模式,这可能表明变量之间的关系不是线性的,或者线性回归模型不适合数据。
残差还用于评估线性回归模型的准确性,并识别可能影响模型质量的异常值或有影响的数据点。
我可以使用多个因变量运行线性回归吗?
在线性回归中,因变量始终是单个变量。但是,您可以有多个自变量。在这种情况下,我们会谈论多元线性回归。
在多元线性回归中,目标是研究多个自变量对单个因变量的影响。
如何解释线性回归中的系数?
在线性回归中,系数表示回归线的斜率和截距。斜率表示自变量每单位变化引起的因变量的变化,而截距表示自变量等于零时因变量的值。
线性回归的数值示例
一个简单的例子可能如下:
假设我们有一组人的以下年龄和身高数据:
| 岁) | 身高(厘米) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| 四五 | 190 |
我们想要确定这些人的年龄和身高之间是否存在关系。为此,我们将使用线性回归。
首先,我们可以用数据绘制统计图(在这种情况下我们建议使用散点图):
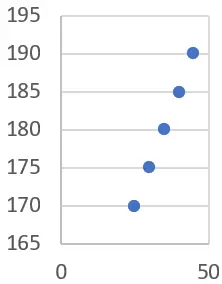
我们可以看到,有一个明显的趋势,随着年龄的增长,身高也随之增加。我们可以通过计算线性回归线来确认这一点。
通过使用我们之前看到的公式计算线性回归线的系数,我们得到:
在 = 145
b = 1
因此,线性回归线的方程为:
身高 = 145 + 1 年龄
我们可以使用这个方程根据一个人的年龄来预测他的身高。例如,如果一个人32岁,我们可以预测他的身高是:
身高 = 145 + 1 32 = 177 厘米