线性函数的导数

在本文中，我们将向您展示线性函数的导数是多少。此外，我们还求解了线性函数导数的几个示例，并演示了此类导数的公式。您甚至可以找到有关线性函数导数的已解决练习。

线性函数的导数是什么？

线性函数的导数是一次项 的系数，也就是说线性函数的导数f(x)=Ax+B等于A。

由于常数的导数为零，因此从导数中删除了独立项。另一方面，一次项的导数是所述项的系数。因此，这两类函数之和的导数就是线性项的系数。

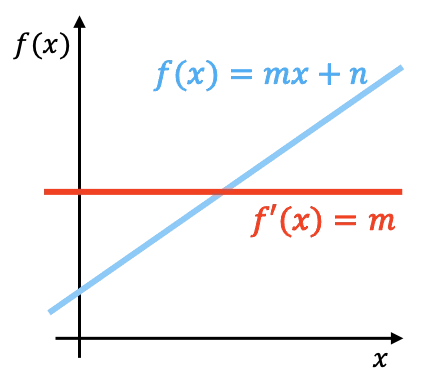
从几何角度来说，线性函数的导数就是该函数的斜率。在上图中，您可以看到表示一个线性函数及其导数。

线性函数的导数示例

给出线性函数导数的定义，我们将计算几个线性函数的例子来完成对概念的理解：

请记住，当函数没有独立项时，或者换句话说，如果它只有一个一级项，则线性函数的导数始终是伴随变量 x 的数字。例如：

因此，线性函数的导数是一个没有自变量的函数，一个简单的数。

线性函数导数的证明

接下来，我们将演示线性函数的导数公式。

令f 为任意线性函数：

计算函数在一点的导数的公式为：

因此，如果我们计算线性函数的前极限，我们会得到：

我们解析括号：

我们用分子来运算：

最后，我们简化分数：

总之，线性函数的导数等于任意点的一次项的系数。由此，导出了线性函数的导数公式。

解决了线性函数的导数问题

计算以下线性函数的导数：

要导出线性函数，只需从函数中消除常数项和变量，仅保留线性项的系数。然而：

尽管函数的系数是分数或根，但线性函数的推导是以相同的方式完成的。