简化分数或约化分数是一种数学过程,旨在将复杂分数转换为另一个更简单的等效分数。因此,这使我们能够找到原始表达式的不可约分数,这可以通过多种方法来完成。但是,在解释它们之前,我们建议您尝试使用本文下方的计算器来简化分数。
在线分数化简
使用以下在线简化分数计算器,您可以减少任何类型的带分数。简单地说,您必须输入分子和分母的值,然后单击简化按钮。完成此操作后,您将获得最简化的表达式。
如何化简分数?
正如我们之前所说,简化分数涉及找到更复杂分数的不可约分数。目前我们有两种化简分数的方法,第一种是普通除法,第二种是提取公因数。
通过除法简化分数
该系统包括将分子和分母除以公约数(1 除外),直到我们不再有公约数,这样我们将得到一个不可约分数。尽管要选择在每次除法中使用的除数,我们可以通过两种不同的方式来完成:第一种是使用公约数,直到我们获得该分数的最简单形式,第二种是计算的最大公约数分子和分母。
例如,如果我们想简化分数 12/64,我们可以通过将分子和分母除以两者的 gcf 来实现,或者将分数的两个部分除以相同的数字,直到得到一个不可约分数,开始具有最小的除数(不包括 1)并向上计算。下面您可以看到这两种方法逐步解决:
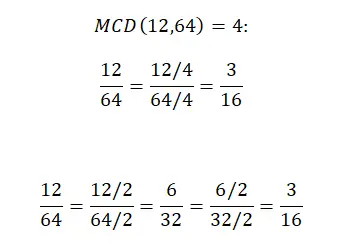
通过公因子提取简化分数
为了执行另一种方法,我们必须将分子和分母分解为素数。我们将原始数值替换为等效幂的乘积。接下来,我们将利用幂的属性,通过简化具有公共基础的幂来继续简化表达式。我们现在将使用此方法简化示例分数:
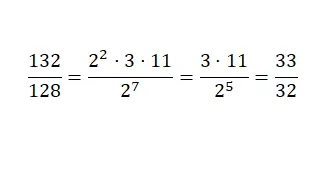
难以减少的分数
接下来,我们将解决有关最复杂的简化情况的一些疑问,这样您将能够减少向您建议的任何分数。虽然这一部分是可选的,但如果您想开始练习,可以跳到最后一部分:
用指数简化分数
为了简化这种类型的分数,我们需要将指数表达式写成单个数值。首先,我们可以尝试素因数分解,简化分子和分母。然后,如果我们还没有得到一个不可约分数,我们将继续将分数的两部分相除,直到得到一个不能再约的表达式。正如您所看到的,用幂简化分数需要结合我们在上一节中讨论的所有方法。
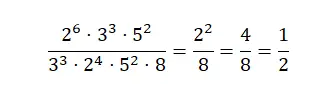
简化负分数
当我们想要简化负分数时,我们可以使用前面解释的三种方法之一来完成,因为符号并不直接影响计算过程。您只需对结果进行一项更改,即添加负号。但是,其他一切都完全相同。为了让您能够看到它,我们在下面向您展示了我们解释的第一个示例,该示例已解决,但带有负号。
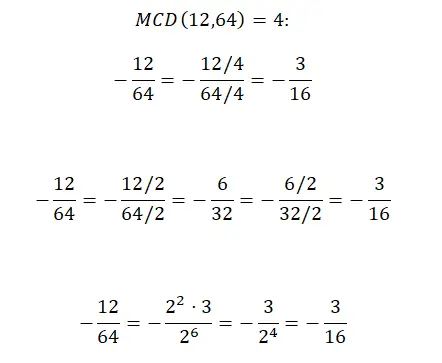
化简大数分数
在这种情况下,我们建议使用公因子提取方法,因为如果用质因子表示大数,它们会变得更容易。因此,您不必解很多除法,直到得到不可约分数。尽管实际上您可以使用您喜欢的任何方法。
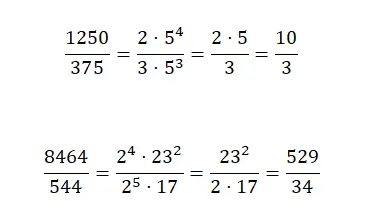
如何用科学计算器化简分数?
在许多科学计算器中,我们可以用更简单的方式表达我们想要的任何分数,只要它不是不可约的。如果是卡西欧科学计算器(学生中最常见的品牌),我们必须按下标有以下表达式“S⇔D”的按钮。由于这一点,我们将能够简化所有类型的表达式,包括分数。在其他品牌中也有一些方法可以做到这一点,但您必须在您的型号手册中查阅它,因为遵循的程序可能会略有不同。

解决了简化分数的练习
这里有一些简化分数的练习,您可以通过它们练习我们已经解释过的不同方法。我们建议您将理论部分与实践同等重要,因为正是通过它,您才能完全理解此类练习中涉及的数学概念。
练习1
化简以下分数,直到找到不可约分数:
在下图中,您将发现使用三种方法之一简化了四个分数。虽然,当您尝试自己减少它们时,您可以使用您喜欢的方法来完成,但重要的是您会得到正确的结果,您应该将其与我们在更正中向您展示的结果进行比较:

练习2
计算以下分数方程中的 x 值:
我们现在提供两个带分数的方程,可以通过化简来求解。这是一个稍微复杂的练习,但是通过应用一些基本的数学概念以及我们在本文中解释的概念,您将能够轻松解决它。
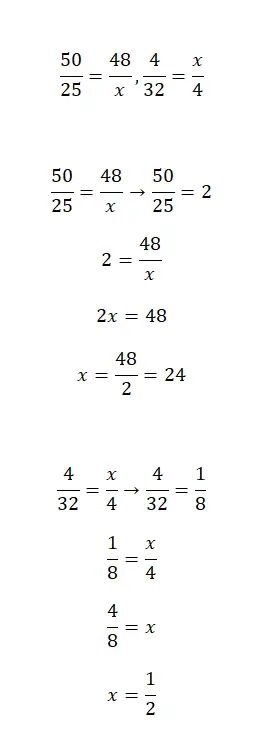
练习3
计算下面所示的每个分数的等效不可约分数:
现在我们挑战你尽可能地简化这些分数,当你解决它们时,你会发现它们比以前的要困难一些。因为,一个包含负号,另一个包含大数值,另一个包含幂。

如果您想要更多分数练习,我们建议您进入最后一个链接,在那里您会发现许多分数问题和运算。通过它您可以练习与分数相关的所有概念。