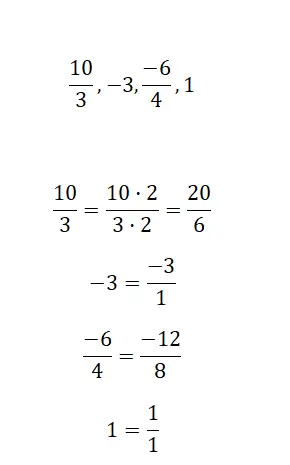在本文中,您将找到有关等值分数或等分分数的解释,非常完整且易于理解。更具体地说,我们将讨论它们的定义、如何计算它们以及如何知道两个分数是否相等。这样,您最终将了解解决等值分数练习所需的一切,就像我们最后将向您展示的练习一样。话虽如此,我们还是从主题开始吧。
等值分数计算器
借助这个等值分数计算器,您将能够检查两个分数是否相等,而无需进行任何计算。它的操作非常简单,基本上你要输入两个分子和两个分母对应的值,然后按“计算”按钮。
什么是等值分数?
等价分数是表示相同数值的分数,因此,即使分子和分母不同,它们也是等价于相同结果的分数。这意味着它们具有比例关系,可以有两种类型:放大或简化。接下来,我们向您展示一个等值分数的图形示例,以便更好地理解这个概念。
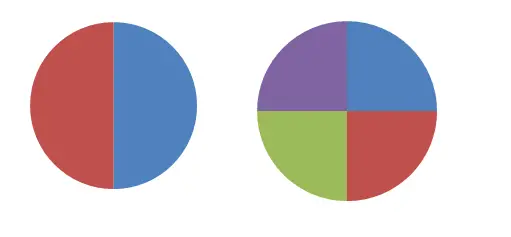
在上图中,您可以看到两个圆圈分为两部分和四部分。如果我们尝试用分数来定义第一个图形,我们会说每个部分等于整体的 1/2,而在第二个图形中我们将使用分数 1/4。显然,这两个分数并不相等,因为它们代表不同的量。但是,如果我们取第二个圆的两部分(2/4),则该表达式相当于 1/2。
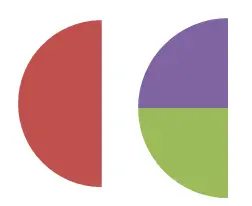
在第二张图中,您可以看到1/2 和 2/4 之间的等价性,也可以通过数值验证。因为 1/2 = 0.5 且 2/4 = 0.5。根据我们之前评论的定义,如果两个分数表达相同的数值,则它们是等价分数。
等值分数的例子
现在我们将向您展示 5 个等值分数的示例。如果您想了解我们如何计算它们,我们建议您继续阅读。
- 相当于二分之一的分数:2/4、3/6、4/8 等。
- 相当于三分之一的分数:2/6、3/9、4/12 等。
- 相当于四分之一的分数:2/8、3/12、4/16 等。
- 等于 1 的分数:4/4、7/7、15/15 等。
- 相当于五分之一的分数:2/10、3/15、4/20 等。
如何计算等值分数?
为了获得等值分数,我们需要将分子和分母乘以或除以相同的数字。因为,如果我们以相同的方式修改分数的两个部分,我们就保持比例关系。因此,我们可以采用两种方法:放大和缩小。
通过放大找到等效分数
在第一种情况下,我们需要将初始分数乘以某个数值。这意味着我们需要将分子和分母乘以这个数字。为了让您可以通过示例看到它,我们向您展示了下面两个等价分数,它们是在进行乘法后获得的:
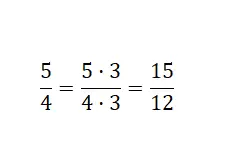
我们所做的是将分数的两个部分都乘以三: 5 x 3 = 15 和 4 x 3 = 12 。因此,我们获得了放大的等效分数,因为它更大。总之,我们找到了一个由不同数值组成的分数,它与原始分数表示相同的数量。
通过化简找到等价分数
其次,我们可以选择通过除以给定分数的分子和分母来简化分数。这样我们就可以得到另一个等价分数,甚至比第一个更简单。然而,值得一提的是,该方法仅在初始表达式不是不可约分数时才有效,因为后者无法进一步约简。下面是通过简化(化简)计算等价分数的示例。
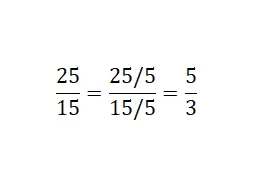
正如您在图片中看到的,我们所做的是将分数的分子和分母除以公约数。在此示例中,我们使用了五个:25/5 = 5 和 15/5 = 3。最后,我们获得了不可约等价分数 25/15。
你怎么知道两个分数是否相等?
为了确定等价分数,我们必须遵循下面将解释的三个程序之一。应该注意的是,第二个与我们在上一节中讨论的分数简化有关。
分子乘以分母
如果您想检查两个分数之间的等价性,可以使用第一个过程。基本上,您必须将第一个分数的分子乘以第二个分数的分母。接下来,您需要将第二个分数的分子乘以第一个分数的分母。如果两个结果相同,那么这些分数将是相等的。看下面的例子:
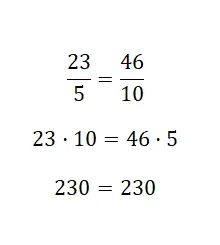
在最后一个例子中,我们验证了这两个分数是等价的。这个例子很容易看出,因为第二个分数是第一个分数的两倍,也就是说,它们具有放大的等价关系。应该注意的是,这个程序使用起来非常方便,只需将叉号相乘就足够了。但我们也建议您学习如何使用其他两个系统,因为这将为您提供更多可用的数学资源。
化简分数
当涉及到不可约分数时,我们可以使用另一种方法,即尽可能地减少由最大数组成的分数。如果在进行这种约简时,我们发现较小的分数是另一个分数的不可约,那么我们可以假设它们是等价的。
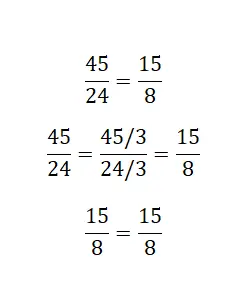
解决并平衡分歧
最后,您可以求助于分数生成的商解,因为带分数始终是除法。基本上,您需要计算两个分数的等价数值,如果数字相同,则它们相等。在下图中,您可以看到一个非常清晰的示例:
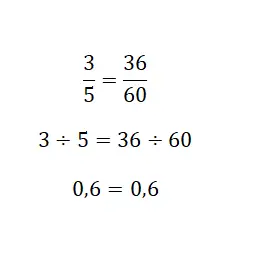
等值分数练习
现在您已经阅读了整个理论,您可以尝试解决以下练习,这将使您完成对解释的理解。我们建议您尝试自己解决这些问题,一旦解决,请将您的结果与我们为您提供的结果进行比较。也就是说,我们让你练习:
练习1
通过化简找到我们提供的每个分数的等价分数:
要解决此练习,只需应用分数简化,即可获得等效的不可约分数。这四个例子非常相似,解决起来没有太大难度。
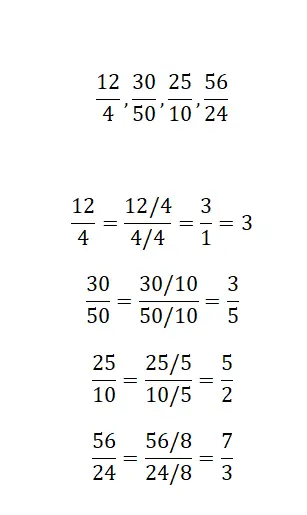
练习2
通过放大我们建议的每个分数找到等效分数:
接下来,您将必须放大我们建议的分数,这样您将获得更大的等效分数。使用什么数字进行乘法并不重要,例如我们将使用 2 和 3 进行乘法。
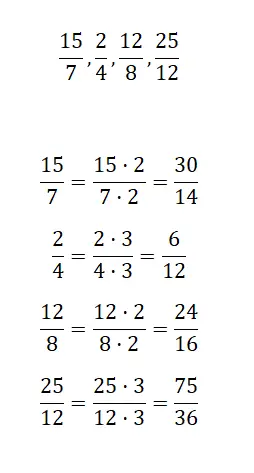
练习3
判断下列分数是否等价:
要确定两个分数是否相等,您需要使用我们上面解释的三种方法之一。尽管您可以自由使用您想要的系统,但您会发现第一个过程已解决了修复问题。
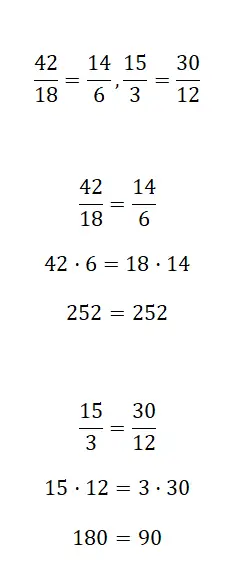
练习4
计算以下表达式的等价分数:
在最后一个练习中,您将必须以分数形式重写我们建议的表达式(整数和带分数),试图保持等价关系。