在此页面上,我们解释了什么是坐标系,此外,您还将找到有关笛卡尔坐标系的所有内容。您还将看到其他类型的坐标系(极坐标系、柱坐标系、球坐标系等)以及坐标系的实际应用。
什么是坐标系?
虽然一开始理解这个概念有点困难,但坐标系的定义是:
坐标系是一个允许我们识别点位置的系统。也就是说,它是一组用于定义任何几何对象的位置的值。
例如,下面的飞机飞行的位置可以用坐标系来描述:
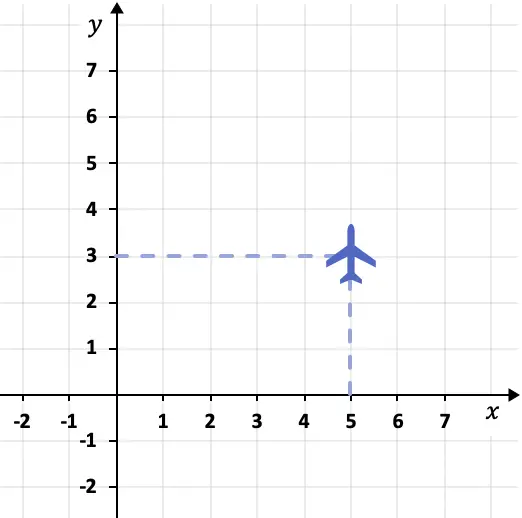
在本例中,平面位于点 (5.3)。因为它的X坐标是5,Y坐标是3。
![]()
另一方面,点 (0,0) 称为坐标原点,因为它是坐标轴的起点,也是坐标系的参考点。
出于好奇,人们认为发明坐标系的数学家是法国人笛卡尔。这就是为什么它也被称为笛卡尔坐标系。
平面内的笛卡尔坐标系
我们在上一节中看到的图形属于平面中的笛卡尔坐标系。我们说它在平面内,因为它是一个二维系统,也就是说它只有两个轴:X轴和Y轴。
X轴对应于水平坐标,而Y轴表示垂直坐标。下面您可以看到以图形方式表示的几个点及其坐标:
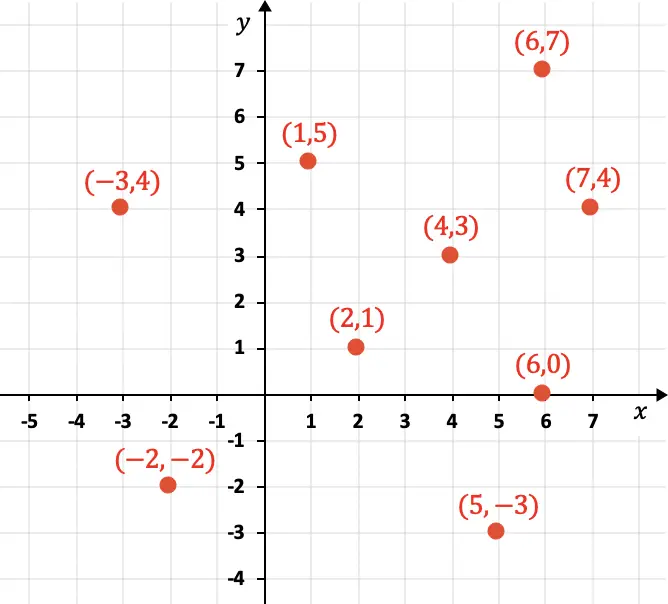
从图中可以看出,坐标是用括号数字表示的,另外,先放X分量,然后放Y分量:(4,3)。此外,坐标可以是正数、负数或零。
另一方面,这种坐标系也称为笛卡尔平面。
最后,您应该知道坐标轴可以有多种表示方式,尽管它们的含义都是相同的:
- X轴也称为横坐标轴或OX轴。
- Y 轴也称为 y 轴或 OY 轴。
空间笛卡尔坐标系
我们刚刚看到了如何表示平面中的点,即在具有两个轴(二维)的坐标系中。然而,现实是由 3 个维度(高度、宽度和深度)组成的。
因此,在欧几里得几何中,三维空间通常由具有三个轴的坐标系表示,所有轴都相互垂直:
- X 轴表示深度。
- Y 轴表示宽度。
- Z 轴对应于高度。
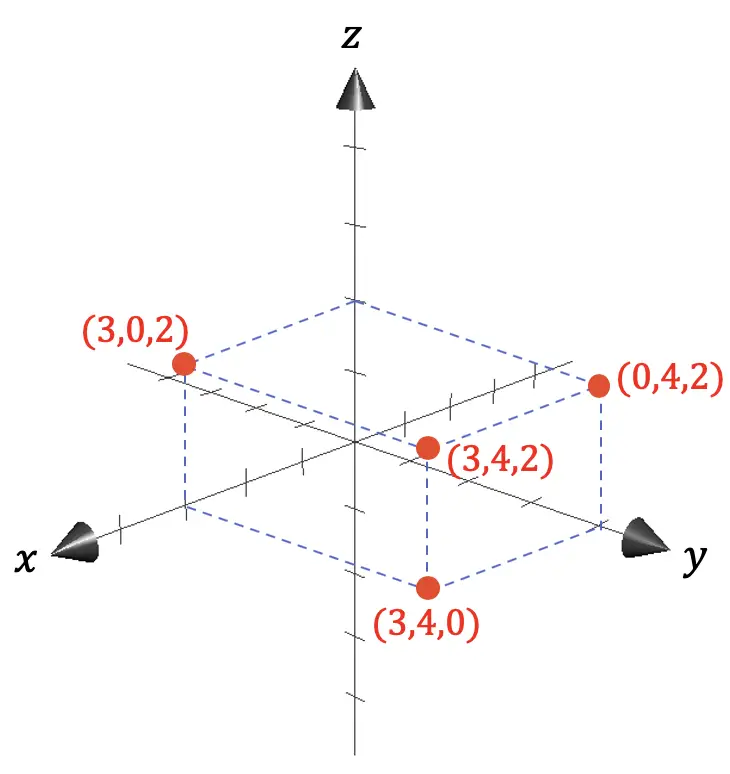
正如您在前面的图形表示中所看到的,任何点的坐标均由相关点与原点 (0,0,0) 之间的距离在轴上的投影给出。
极坐标系
笛卡尔坐标系(2D 或 3D)使用最广泛。但在某些情况下,我们使用另一种坐标系可能会更方便。
极坐标系是一个二维参考系,其坐标为:
-

是坐标原点到该点的距离。这称为径向坐标。
-

是 X 轴与穿过该点的直线与原点所成的角度。这称为角坐标或方位角坐标。
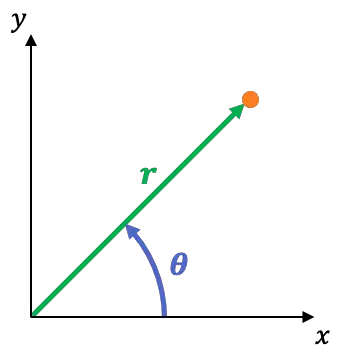
您可以使用以下等式轻松从直角坐标系切换到极坐标系:
将极坐标转换为笛卡尔坐标
![]()
![]()
从笛卡尔坐标切换到极坐标
![]()
![]()
圆柱坐标系
柱坐标系与极坐标系非常相似。事实上,它是同一件事,但多了一个坐标:高度。
因此,圆柱框架是三维框架,也就是说具有 3 个坐标:
-

是点在 XY 平面上的正交投影,或者换句话说,是点到 Z 轴的距离。
-

是正半轴的角度

-

是点的高度,是空间中笛卡尔坐标系的同坐标。
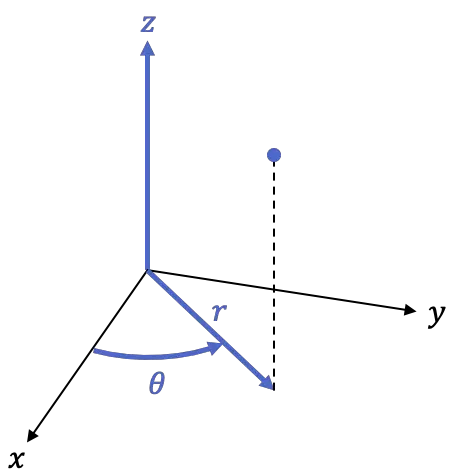
下面的公式用于将笛卡尔坐标系转换为柱坐标系:
将柱坐标转换为笛卡尔坐标
![]()
![]()
![]()
将笛卡尔坐标转换为柱坐标
![]()
![]()
![]()
球坐标系
最后,我们有了球坐标系。这种坐标系也与极坐标和柱坐标系非常相似,尽管显然与它们有一些区别。
球坐标系是描述三维欧几里得空间的系统,因此,它具有三个坐标:
-

是从原点到该点的距离(以 R3 为单位)。
-

是 X 轴的正值部分与直线形成的角度

投影到 XY 平面。
-
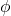
是 Z 轴正值部分与直线之间的角度

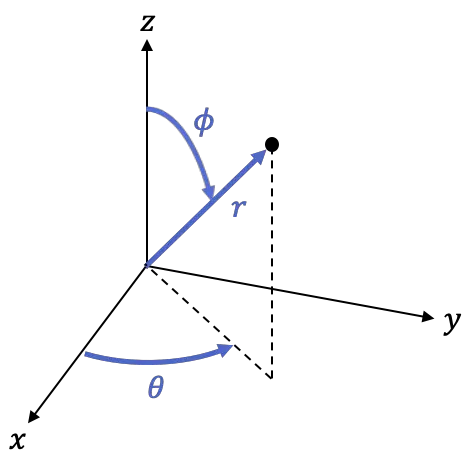
您可以使用以下公式在球坐标和笛卡尔坐标之间切换:
将球坐标转换为笛卡尔坐标
![]()
![]()
![]()
将笛卡尔坐标转换为球坐标
![]()
![]()
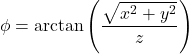
坐标系的实际应用
坐标系在数学中非常重要,因为它们也在现实生活中使用。例如,它们对于在地图上定位物体、人甚至地点非常有用。事实上,GPS 的存在是因为坐标系,因为它们用坐标系来了解您在地球上的位置。
更准确地说,GPS 地理坐标由两个元素组成:纬度和经度。纬度(北或南)和经度(东或西)是两个角坐标,用于测量地球中心与您所在位置之间的角度。两者都以度为单位,以十进制或六十进制坐标表示。