在此页面上,您将找到有关空间解析几何(以及公式)的所有内容的解释:直线和平面的方程、平面和直线之间的相对位置、如何计算空间中的距离和角度,…
什么是空间几何?
空间几何是几何学的一个分支,负责研究三维(3D)几何图形,即那些在空间中占据一席之地的图形。如圆锥体、立方体、棱锥体、球体、圆柱体、棱柱、多面体等。
然而,在本页中,我们将重点关注空间中的解析几何,即空间几何的一部分,重点分析点、线、面、两个几何图形之间的距离、它们形成的角度、不同几何图形之间的交点人物。元素等
空间直线方程
回想一下,直线的数学定义是一组沿相同方向表示的连续点,没有曲线或角度。
因此,为了以数学方式表达三维空间(在 R3 中)中的任何直线,我们使用该直线的方程,并且为了找到它们,我们只需要属于该直线的点和该直线的方向向量。

仅用这两个几何元素,就可以求出该直线的所有不同方程,如下:
直线方程为矢量方程、参数方程、连续方程和隐式(或一般)方程。
下面是对不同类型直线方程的解释。
空间线的向量方程
是的
![]()
是直线的方向向量,
![]()
属于右边的点:
![]()
直线的矢量方程的公式为:
![]()
空间线的参数方程
我们可以通过将分量与分量相等,从直线的矢量方程得到直线的参数方程的公式:
![]()
空间直线的连续方程
直线连续方程的公式为:
![]()
这类直线方程也可以从参数方程中得到,您可以在我们的连续方程页面上看到演示,此外,您还可以从右侧看到方程求解练习的示例和练习。
空间直线的一般(或隐式)方程
最后,通过将直线连续方程的分数乘以二,我们得到直线 的一般(或隐式)方程:
![]()
这种类型的直线方程也称为笛卡尔方程。
我们刚刚看到了 4 个最相关的直线方程(向量方程、参数方程、连续方程和一般方程),然而,还有另一个有些特殊的方程,因此需要整整一页的时间来解释它。这是规范方程,在此链接中您可以看到它的完整解释,为什么它如此特别以及它与其他方程的不同之处。
空间平面方程
在解析几何中,平面方程是允许任何平面以解析方式表达的方程。因此,要找到平面的方程,您只需要一个点和属于该平面的两个线性无关向量。

因此,所有类型的平面方程为:矢量方程、参数方程、隐式(或一般)方程和平面的正则(或分段)方程。
接下来我们将看到该计划所有方程的解释和公式。
平面的向量方程
给定一个点和平面的两个方向向量:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面矢量方程的公式为:
![]()
或同等学历:
![]()
金子
![]()
和
![]()
它们是两个标量,也就是说两个实数。
平面参数方程
另一方面,平面参数方程的公式为:
![]()
平面的隐式或一般方程
计划的隐式方程,也称为一般方程,通过求解以下行列式并将结果设置为 0 得到:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
因此,所得计划的隐式或一般方程将具有以下形式:
![]()
此类平面方程也称为笛卡尔平面方程。
平面的正则方程或分段方程
平面的正则或分段方程的公式如下:
![]()
金子:
-

这是平面和 X 轴之间的交点。
-

这是平面和 Y 轴之间的交点。
-

这是平面与 Z 轴相交的位置。
垂直于平面的向量
垂直于平面的向量是垂直于该平面中包含的所有直线的向量。因此,垂直于平面的矢量意味着它垂直于该平面。
空间解析几何中的许多度量问题都涉及平面及其法向量。要解决这些练习,您只需要知道平面与其法向量之间的数学关系:
垂直于平面的矢量的分量X、Y、Z分别与所述平面的隐式(或一般)方程的系数A、B、C一致。
![]()
金子
![]()
是与平面正交的向量
![]()
空间中两个几何元素的相对位置
显然,一条线或一个平面不一定必须在空间中单独存在,相反,它们通常会相互作用:它们相交、平行、垂直等。好吧,在本节中我们将看到直线和平面的不同相对位置以及它们是如何确定的。
两条线在空间中的相对位置
在解析几何中,当在三维空间(在 R3 中)中工作时,两条线之间有 4 种可能的相对位置:两条线可以是重合线、平行线、割线或割线。
平行线

如果两条线具有相同的方向但没有公共点,则它们是平行的。此外,平行线彼此之间的距离始终相同。
重合线

如果两条线具有相同的方向并且它们的所有点都是公共的,则两条线重合。
交叉线

两条相交线方向不同,但交于一点。
交叉线

两条相交线的方向不同,并且在任何一点都不相交。因此两条交叉线不在同一平面上。例如,在线上方的图形表示中
![]()
总是在直线前面
![]()
,所以他们永远不会互相接触。
如何通过范围查找两条线的相对位置
查找两行相对位置的一种方法是计算两个特定矩阵的范围,如下所示。当两条直线以隐式(或一般)方程的形式表示时,此方法非常有用。
因此,如果我们有两条线用三维空间(在 R3 中)中的隐式(或一般)方程表示:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-500405383e97627c17d01023fd9dd198_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c96b6990dae5ce476ee55689cf4f4fb_l3.png)
设 A 为两条线的系数组成的矩阵:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9199790c5f157691d9307604f25fc873_l3.png)
并给出扩展矩阵A’,它是两条线的所有参数组成的矩阵:
![Rendered by QuickLaTeX.com \displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f087aea2d9209341c2acf240eab2bc77_l3.png)
然后,根据前两个矩阵的范围,可以根据下表确定两条线的相对位置:

因此,为了找到两行之间的相对位置,我们必须计算两个矩阵的范围,并且根据每个矩阵的范围,这将是一种情况或另一种情况。
这个定理可以使用 Rouché-Frobenius 定理(一种用于求解线性方程组的方法)来证明,但是在本页中我们不会进行证明,因为它相当麻烦并且没有增加太多内容。 。
两个平面在空间中的相对位置
在解析几何中,两个平面之间只有三种可能的相对位置:相交平面、平行平面和重合平面。
- 相交平面:如果两个平面仅相交于一条直线,则它们相交。
- 平行平面:如果两个平面在任何一点都不相交,则它们平行。
- 重合平面:如果两个平面有所有公共点,则两个平面重合。
相交镜头

平行平面

配套方案

如何通过系数确定两个平面的相对位置
了解两个平面之间相对位置的一种方法是使用它们的一般(或隐式)方程的系数。
然后考虑两个不同平面的一般(或隐式)方程:
![]()
![]()
三维空间中两个平面之间的相对位置取决于它们的系数或参数的比例:

因此,当系数 A、B 或 C 之一与其他系数不成比例时,两个平面将相交。另一方面,当只有独立项不成比例时,两个平面将平行。最后,当两个方程的所有系数成比例时,计划将重合。
空间距离
下面有计算不同几何元素之间距离的公式:点和线之间、两个平面之间、平面和线之间……
两点之间的距离
两点之间的距离对应于由这两点确定的向量的范数。
因此,如果我们有两个通用点:
![]()
两点之间的距离的公式为:
![]()
点到线的距离
空间中一点到直线距离的计算公式为:
![]()
金子:
-

是直线方向向量的模

-

是右边的一个点


线上的一个点

和

由两点定义的向量
-

是向量之间向量积的模

和

两条线之间的距离
两条线之间的距离取决于它们的相对位置:
- 如果两条线重合或相交,则两条线之间的距离等于零,因为它们(至少)相交于一点。
- 当两条线平行或相交时,必须根据情况应用公式(两种解释均在下面提供)。
两条平行线之间的距离
两条平行线的距离始终相同。因此,要计算空间中两条平行线之间的距离(在 R3 中),其方式与在平面中(在 R2 中)相同:您只需在两条线上取一点并找到那里的距离就是从这一点到另一条线。

因此,要确定两条平行线之间的距离,必须使用点和线之间的距离公式。
两条相交线之间的距离
设方向向量和两条相交线的任意点为:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-569f8d554a0f3704d247862d0b8ef852_l3.png)
两条相交线之间的距离的公式为:
![]()
金子:
-
![Rendered by QuickLaTeX.com \left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|](https://mathority.org/wp-content/ql-cache/quicklatex.com-dbc3e38427d29b2f4444ea732f955500_l3.png)
是向量混合积的绝对值
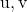
以及由点定义的向量

和

。
-
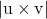
是两条交叉线的方向向量之间的向量积的模。
尽管这里有公式,但确定两条相交线之间的距离比看起来更复杂。因此,如果您想在以下链接中进行练习,您可以查看有关两条相交线之间的距离的示例和已解决的练习。
点到平面的距离
给定一个点和平面的一般(或隐式)方程:
![]()
点到平面的距离公式为:
![]()

如果通过应用该公式我们得到的结果等于零,这显然意味着该点和平面之间的距离为零,因此该点是该平面的一部分。
两个平面之间的距离
空间中两个平面之间的距离取决于这两个平面之间的相对位置:
- 如果两个平面相交或重合,则它们之间的距离等于零,因为它们相交于某一点。
- 如果两个平面平行,则通过在两个平面之一上取一点并计算该点与另一个平面之间的距离来计算两个平面之间的距离。
两个平行平面之间的距离
两个平行平面彼此之间的距离始终相同,因此要找到两个平行平面之间的距离,我们可以在两个平面之一上取一个点,然后计算从该点到另一个平面的距离。

因此,要计算两个平行平面之间的距离,您必须在两个平面之一上找到一个点,然后使用点与平面之间的距离公式。
空间中的角度
与距离一样,确定空间中两个几何对象之间的角度取决于它们的几何特征。因为计算两条直线形成的角度与计算两个平面形成的角度不同。下面是求直线和平面之间角度的公式。
两条线之间的角度
要知道欧几里德空间中两条线之间的角度,我们必须计算它们的方向向量形成的角度,因此:
给定两条不同直线的方向向量:
![]()
这两条线形成的角度可以用以下公式计算:
![]()
金子
![]()
和
![]()
是向量的模
![]()
和
![]()
分别。
回想一下向量模的公式是:
![]()
两个平面之间的角度
两个平面之间的角度等于所述平面的法向量形成的角度。因此,为了找到两个平面之间的角度,我们计算它们的法向量形成的角度,因为它们是相等的。
给定两个不同平面的一般(或隐式)方程:
![]()
![]()
每个平面的法向量为:
![]()
![]()
这两个平面形成的角度是通过使用以下公式计算它们的法向量形成的角度来确定的:
![]()
直线和平面之间的角度
直线与平面所成的角定义为直线的方向向量与平面的法向量所成的两个余角中的较小者。
因此,如果
![]()
是直线的方向向量,
![]()
是垂直于平面的向量:
![]()
![]()
用于计算直线和平面所成角度的公式为:
![]()