空间中直线到平面的距离

在这里，您将了解如何计算从直线到平面的距离，此外，您还可以看到逐步解决的示例和练习。

直线和平面之间的距离是多少？

在解析几何中，空间中直线和平面之间的距离取决于这两个几何元素之间的相对位置：

如果直线包含在平面内或者直线和平面平行，则它们之间的距离为零。
如果直线与平面平行，则通过取直线上的任意一点并计算该点到平面的距离即可找到直线到平面的距离。

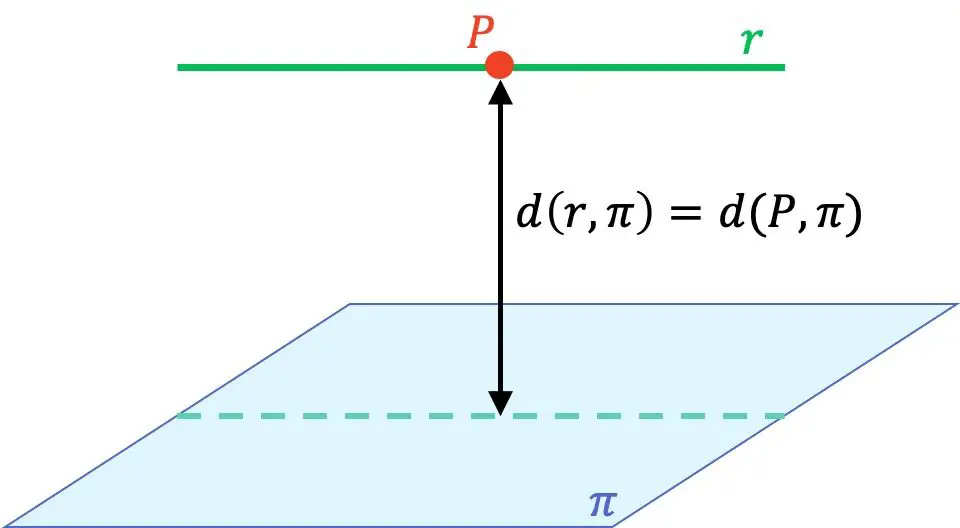
因此，要计算直线到平面的距离，必须知道如何确定直线和平面之间的相对位置以及如何计算点和平面之间的距离。因此，如果您不完全清楚或不知道公式，我们建议您首先查看链接的页面，您将在其中找到解释、示例和逐步解决的练习。

计算直线和平面之间的距离的示例

为了让您了解如何求空间中直线和平面之间的距离（在 R3 中），我们将解决一个问题作为示例：

线路有多远
$r$

在飞机上

$\pi$

？

$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

要求直线和平面之间的距离，首先必须知道两者之间的相对位置。

一方面，直线以参数方程的形式定义，所以它的方向向量和它经过的点是：

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

另一方面，垂直于平面的矢量为：

$\vv{n} =(4,2,1)$

因此，要确定平面和直线的相对位置，需要计算直线的方向向量和平面法线向量之间的标量积：

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

点积的结果为零，因此直线只能包含在平面内或与平面平行。因此，为了找出是哪种情况，我们将直线上的点的笛卡尔坐标代入平面的方程中：

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

将直线上的点代入平面方程中，我们得到一个不等式，因此该点不遵守平面方程，因此直线和平面是平行的。

一旦我们知道直线和平面平行，我们就可以计算它们之间的几何距离。为此，我们取直线上的点并计算从该点到平面的距离。

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

因此，我们使用点到平面的距离公式：

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

现在我们将每个未知数的值代入公式：

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

最后，我们执行以下操作：

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

这样直线到平面的距离就相当于计算出的点到平面的距离：

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

显然，距离必须总是给我们一个正值，因为距离总是正值。如果我们得到否定的结果，则意味着我们在采取步骤时犯了错误。

直线和平面之间的距离是多少？

计算直线和平面之间的距离的示例

发表评论 取消回复

发表评论取消回复