在此页面上,您将找到有关直线显式方程的所有信息:它是什么、它的公式是什么、计算示例等。您还将找到关于斜率含义和显式方程截距的详细解释。而且,更重要的是,您将看到不同的示例,并且能够通过逐步解决的练习进行练习。
直线的显式方程是什么?
请记住,直线的数学定义是一组连续的点,这些点以相同的方向表示,没有曲线或角度。
因此,显式直线方程是一种用数学方式表达任何直线的方法。为此,您只需要知道直线的斜率及其与 Y 轴的相交点。
直线的显式方程的公式
直线的显式方程的公式为:
![]()
金子
![]()
是直线的斜率,
![]()
它的 y 轴截距,即与 Y 轴相交的高度。
我们通过一个例子来看一下直线的显式方程是如何计算的:
- 写出经过该点的直线的显式方程
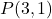
斜率m=2。
直线的显式方程的公式为:
![]()
在这种情况下,该语句告诉我们直线的斜率是 m=2,因此直线的方程如下:
![]()
因此计算系数n就足够了。为此,我们必须将属于该线的点代入其方程中。在这种情况下,该语句告诉我们该线穿过该点
![]()
然而:
![]()
![]()
我们求解得到的方程来找到 n 的值:
![]()
![]()
![]()
![]()
因此,该直线的显式方程为:
![]()
请记住,除了显式方程之外,还有其他方法可以解析地表达直线。例如,向量方程,它是一种与其他直线方程不同的直线方程,因为方向向量和直线上的点用它们自己的坐标表示。在链接中您可以看到它是什么以及为什么它如此特别。
参数m和n的含义
正如我们在直线的显式方程的定义中看到的,参数
![]()
是直线的斜率,
![]()
它的 y 轴截距。但是,这是什么意思?让我们从一条线的图形表示中看到这一点:

独立一词
![]()
是直线与计算机轴(OY 轴)的交点。在上图中
![]()
等于 1,因为该线与 y 轴相交于 y=1。
另一方面,术语
![]()
表示线的斜率,即它的倾角。正如您在图表中看到的那样,
![]()
等于 2,因为 1 个水平单位,直线上升 2 个垂直单位。
显然,如果斜率为正,则函数增加(上升),反之,如果斜率为负,则函数下降(下降)。
计算直线的斜率
此外,有 3 种不同的方法可以用数值确定直线的斜率:
- 给定线上两个不同的点

和

直线的斜率等于:
- 是的

是直线的方向向量,其斜率为:
- 是的

是直线与横坐标轴(X 轴)形成的角度,直线的斜率等于该角度的正切:
![]()
![]()
![]()

线的相对位置
最后,一条线的斜率还可以用来了解多条线之间的关系。由于两条平行线具有相同的斜率,另一方面,如果一条线的斜率是另一条线的斜率的负倒数,则意味着这两条线是垂直的。


计算经过两点的直线的显式方程
一个非常典型的问题是在给定直线经过的两个点的情况下找到该直线的显式方程。我们通过一个例子看看是如何解决的:
- 确定经过以下两点的直线的显式方程:
![]()
要找到直线的显式方程,您需要知道参数 m 和 n 的值。所以我们首先使用冒号公式计算直线的斜率:
![]()
![]()
然后我们可以通过将直线上的点代入方程来找到 y 截距:
![]()
![]()
![]()
![]()
![]()
所以该直线的显式方程为:
![]()
从隐式方程求显式方程
最后,我们经常遇到的另一类问题是从隐式方程(也称为一般方程或笛卡尔方程)中找到直线的显式方程。显然,要理解以下方法,您需要确切地知道隐含方程是什么以及它是怎样的;但如果你根本不记得了,你可以在链接中查看。
因此,如果您已经掌握了直线的隐式(或一般)方程,让我们看看这个过程是如何工作的:
- 求下列直线的显式方程:
![]()
要找到直线的显式方程,我们所要做的就是求解变量
![]()
所以我们通过条款没有
![]()
等式的另一边:
![]()
现在我们清除变量
![]()
![]()
最后,我们简化一下:
![]()
![]()
![]()
因此这条线的斜率是
![]()
其 y 轴截距为 4。
解决显式方程问题
练习1
给出下列直线的斜率和 y 截距:
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3077643710747855c7b59a93551fbad8_l3.png)
直线的显式方程如下:
![]()
金子
![]()
是斜率并且
![]()
计算机位于原点。然而:
![Rendered by QuickLaTeX.com \bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62bc45bc23ea6c323b1a5d95ba40ca2_l3.png)
![Rendered by QuickLaTeX.com \bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-683f74baf43275be7565fc744704e6ed_l3.png)
![Rendered by QuickLaTeX.com \bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39e8a1c6dbe8e5ff8db1fc8b08c4c95d_l3.png)
最后一行由其隐式方程表示,因此我们首先需要将其传递给显式方程(求解
![]()
)然后我们可以识别参数:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{cases} m = -2 \\[2ex] n=3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50c2bb75ae362e0a2dee3a3670459df3_l3.png)
练习2
求通过该点的直线的显式方程
![]()
并且有斜率
![]()
直线的显式方程的公式为:
![]()
在这种情况下,直线的斜率必须为 -2,因此直线方程将具有以下形式:
![]()
因此计算系数n就足够了。为此,您必须将属于该线的点代入其方程并求解所得方程:
![]()
![]()
![]()
![]()
![]()
简而言之,该直线的显式方程为:
![]()
练习3
求通过以下两点的直线的显式方程:
![]()
要找到直线的显式方程,您需要知道参数 m 和 n 的值。因此,我们首先根据两点的坐标计算直线的斜率:
![]()
![]()
然后我们通过将直线上的一点代入方程来确定截距:
![]()
![]()
![]()
![]()
所以该直线的显式方程为:
![]()
练习4
计算与 X 轴形成 45° 角并通过坐标原点的直线的显式方程。
如果直线与 OX 轴成 45 度角,则其斜率为:
![]()
![]()
一旦我们知道了直线的斜率,我们就可以通过将直线上的点代入方程来计算 y 截距。另外,该语句告诉我们,直线经过坐标原点,这意味着它经过点(0,0)。然而:
![]()
![]()
![]()
所以该直线的显式方程为:
![]()
练习5
求与直线平行的直线的显式方程
![]()
以及整个过程中会发生什么
![]()
说直话
![]()
![]()
使得线与线平行
![]()
两者必须具有相同的斜率,因此:
![]()
![]()
一旦我们知道了直线的斜率,我们就可以通过将属于直线的点代入方程来计算 y 截距:
![]()
![]()
![]()
![]()
![]()
所以该直线的显式方程为:
![]()
练习6
每条图形线的显式方程是什么?

蓝色右
蓝线每增加一个 Y
![]()
右绿色
绿线对于每个 X 增加 3 Y,因此其斜率为 3。此外,该线与 Y 轴相交于 -4,因此其 y 截距为 -4。
![]()
红线
每增加一个 X,红线就会减少 2 个 Y,因此它的斜率是 -2。并且该线与 y 轴相交于 y=-2,因此它的 y 截距也是 -2。
![]()