在此页面上,您将找到直线斜率最详细的解释:其公式是什么、计算示例、直线斜率的概念意味着什么……您还将能够看到如何轻松识别斜率从方程中画出一条直线,此外,您还可以通过逐步解决的练习进行练习。
直线斜率的公式
直线的斜率等于两点之间的垂直位移除以这两个点之间的水平位移。
也就是说,给定一条线上的两个点:
![]()
直线斜率的公式为:
![]()
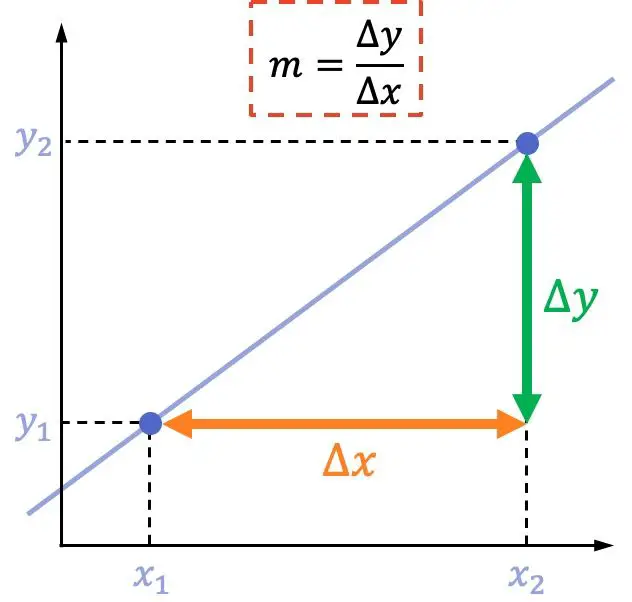
计算两点直线斜率的示例
接下来,我们将看到一个如何使用以下公式计算直线斜率的示例:
- 计算经过以下两点的直线的斜率:
![]()
要找到这条线的斜率,只需应用其公式:
![]()
因此,该线的斜率等于 3。
从方程求出直线的斜率
在上面的部分中,我们刚刚了解了如何以数值方式确定直线的斜率。然而,并不总是需要进行计算,也可以从直线方程中确定其值。每种类型的方程都不同,因此我们将分别分析每种情况。
给定直线的显式方程的斜率
该直线的显式方程如下:
![]()
然后是参数
![]()
对应于线的斜率。
给定直线的点斜率方程的斜率
直线的点斜率方程公式如下:
![]()
和之前一样,系数
![]()
对应于线的斜率。
给定直线隐式方程的斜率
给定直线的隐式方程(也称为一般方程或笛卡尔方程):
![]()
可以通过执行以下操作找到该线的斜率:
![]()
考虑线的方向向量的斜率
线的方向向量是标记其方向的向量。因此,如果一条线的方向向量为:
![]()
这条线的斜率是:
![]()
给定角度的斜率
最后,如果一条线形成一个角度
![]()
在横坐标轴(X轴)的正值部分,其斜率等于角度的正切:
![]()
直线斜率的含义
有了上述所有信息,我们已经非常清楚如何找到直线的斜率。但实际上……直线的斜率是什么意思?
直线的斜率表示该直线相对于图形的每个水平单位上升的垂直单位。
例如,在下面的线的表示中,您可以看到每个水平单位前进 2 个垂直单位,因为它的斜率等于 2。

此外,直线的斜率也表示其陡峭程度:
- 如果一条线正在增加(上升),则其斜率为正。
- 如果一条线呈递减(下降)趋势,则其斜率为负。
- 如果一条线完全水平,则其斜率等于 0。
- 如果一条线完全垂直,则其斜率等于无穷大。


线的相对位置
另一方面,两条线之间的相对位置也可以从斜率的性质得知:
- 如果两条线有不同的斜率,这意味着它们相交,即它们相交于一点。
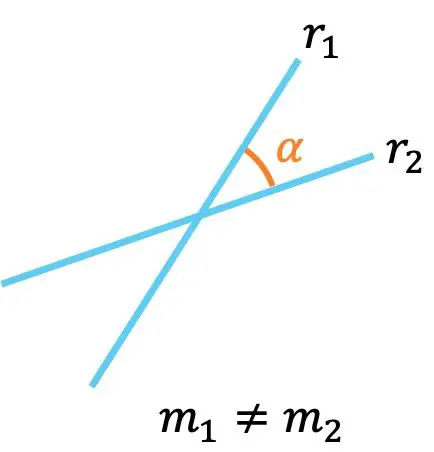
此外,两条线与斜线之间的角度可以用以下公式计算:
![]()
- 其次,如果两条线具有相同的斜率,则意味着它们是平行的。

- 最后,两条垂直或正交线(形成 90°)的斜率满足以下条件:

这是确定两条线是否相互平行或垂直的一种方法,但是,还有其他方法,有些甚至更快。要了解更多信息,您可以转到线之间的垂直度和平行度的解释。此外,这些页面还解释了如何找到与另一条垂直(或平行)的线。
解决了直线的斜率问题
练习1
求通过以下两点的直线的斜率:
![]()
要计算直线的斜率,必须使用以下公式:
![]()
练习2
计算经过以下两点的直线的斜率:
![]()
要找到直线的斜率,您必须使用以下公式:
![]()
练习3
每条线的斜率是多少?
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d405c8176957af59906c98149714570_l3.png)
A)该直线表示为隐式方程,因此其斜率为 2 (伴随该方程的项)
![]()
)。
B)该线由其点斜率方程定义,因此其斜率为 4 (括号前的数字)。
C)该直线为隐式方程形式,因此其斜率为:
![]()
D)直线是以参数方程的形式定义的,所以我们首先必须找到它的方向向量,然后用它我们可以计算直线的斜率。因此,方向向量的分量是伴随系数的项
![]()
![]()
一旦我们知道了直线的方向向量,我们就可以确定直线的斜率:
![]()
练习4
确定每条图形线的斜率:

蓝色右
蓝线每 X 增加 1 个 Y,因此其斜率等于 1。
![]()
右绿色
绿线每 X 增加 3 个 Y,因此其斜率为 3 。
![]()
红线
每增加一个 X,红线就会减少 2 个 Y,因此它的斜率等于 -2 。
![]()