余弦导数

在这里您将了解如何导出余弦函数（公式）。您将能够看到余弦函数导数的示例，并通过逐步练习进行练习。此外，我们还向您展示了公式的证明，什么是余弦的二阶导数，甚至是反余弦的导数。

余弦的导数是什么？

余弦函数的导数是符号修正的正弦函数。换句话说，x的余弦导数等于减去x的正弦。

如果余弦参数中有一个函数，则余弦的导数是减去该函数的正弦值乘以该函数的导数的乘积。

第二个公式与第一个公式等效，但应用了链式法则。所以，综上所述，余弦导数的公式如下：

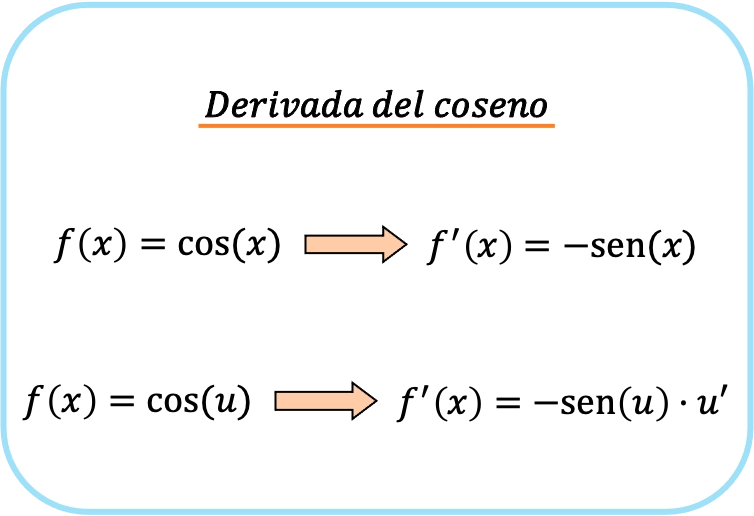
余弦导数示例

现在我们知道了余弦公式是什么，我们将解释此类三角导数的几个例子，以便您对如何推导余弦函数不再有疑问。

示例 1：2x 余弦的导数

在余弦参数中，我们没有单个 x，而是一个更复杂的函数。因此，我们需要使用下面的公式来推导余弦：

由于 2x 的导数为 2，因此 2x 的余弦导数将减去 2x 的正弦乘以 2。

示例 2：x 平方余弦的导数

与前面的示例一样，在余弦参数中，我们有一个与 x 不同的函数，因此我们将使用链式法则来导出余弦：

那么，x ²的导数为 2x，因此，x 的余弦的 2 次方导数为：

示例 3：余弦三次方的导数

本例中的余弦函数是由另一个函数组成的，因此我们需要应用以下公式来求解导数：

因此，通过应用公式，我们得到函数的导数：

➤为了对该函数求导，还必须使用势函数的导数公式。

余弦的二阶导数

接下来，我们将看到，由于三角函数的特性，正弦的二阶导数可以很容易计算。

➤注意：要理解下面的内容，你需要知道什么是正弦的导数。

x 的余弦二阶导数减去 x 的余弦。这可能看起来很奇怪，但从数学上来说确实如此。事实上，正弦的导数是余弦，因此，通过对 x 的余弦求两次微分，可以再次获得余弦，但符号有所改变。

如果余弦参数不是 x，则此属性会发生变化，因为在这种情况下我们拖动链式法则的项：

反余弦的导数

所有三角函数都有反函数，因此余弦函数也可以反函数。同样，反余弦是可微的。

函数的反余弦导数减去该函数的导数除以一的平方根减去该函数的平方。

请记住，反余弦也称为反余弦。

例如，3x 的反余弦导数为：

解决了余弦导数的练习

计算以下余弦函数的导数：

余弦导数的证明

最后，我们将以数学方式演示 x 余弦导数的公式。为此，我们将使用导数的定义，它对应于以下限制：

我们要证明余弦，所以函数是 cos(x)：

我们不能通过替代来解决这个限制，因为我们最终会陷入不确定性。但是，我们可以通过应用以下三角恒等式以另一种方式表达总和的余弦：

下一步是将分数分成两个分数并取余弦的公因数：

减法的极限等于极限的减法，因此：

x 的余弦和 x 的正弦不依赖于 h，因此我们可以将它们提取到界限之外：

通过无穷小当量计算极限，我们得出第一个极限为 0，第二个极限为 1。因此：

至此我们已经得到了余弦函数导数的公式，因此等式得到证明。