在本页中,我们解释什么是线性无关向量和线性相关向量。您还将看到如何判断一组向量是线性相关还是独立的示例。此外,您还将找到有关线性独立性和依赖性的练习并逐步解决问题。
什么是线性无关向量?
如果一组自由向量中没有一个可以写成其他向量的线性组合,则它们是线性独立的。
换句话说,给定一组向量
![]()
如果以下方程的唯一解是线性独立的:
![]()
这些都是所有的系数
![]()
等于0:
![]()
几何上,如果两个向量不具有相同的方向,即不平行,则它们是线性无关的。
为了简洁起见,我们有时直接说它们是 LI 向量。或者向量具有线性独立性。
什么是线性相关向量?
显然,线性相关向量的含义与线性无关向量相反。因此它的定义是:
如果平面的一组自由向量中的任何一个可以表示为形成系统的其他向量的线性组合,则它们是线性相关的。
换句话说,给定一组向量
![]()
如果存在以下方程的解,则这些是线性相关的:
![]()
其中有一定的系数
![]()
与 0 不同:
![]()
反之亦然:如果一个向量是其他向量的线性组合,则该集合中的所有向量都是线性相关的。
此外,如果两个向量平行,则意味着它们是线性相关的。
有时它们也被缩写并简称为 LD 向量。或者甚至向量具有线性相关性。
如何知道向量是否线性相关或独立的示例
然后我们将看到线性相关向量和独立向量的典型示例。
- 确定以下 3 个 3 维向量是否具有线性相关性或独立性:
![]()
![]()
![]()
首先,我们需要说明线性组合条件:
![]()
现在我们用每个向量的坐标替换它。和零一样,对应零向量:
![]()
系数乘以向量,因此以下表达式是等效的:
![]()
我们添加向量:
![]()
如果我们仔细观察,前面的表达式对应于 3 个方程,因为左向量的每个坐标必须等于右向量的每个坐标。因此,我们有一个由 3 个方程和 3 个未知数组成的齐次方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c6bb8117dd8ae715314efe73fe65eed8_l3.png)
所以我们唯一需要做的就是求解未知数为的方程组
![]()
和
![]()
为此,您可以使用任何方法(替换法、高斯法、克莱默法则等)。然而,要知道向量是 LI 还是 LD,只需确定是否存在除平凡解(所有系数都为零)之外的解就足够了。所以:
- 如果由向量分量组成的矩阵的行列式不为零,则意味着方程组只有一个解(
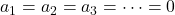
),因此向量是线性无关的
- 另一方面,如果由向量分量组成的矩阵的行列式等于零,则意味着方程组具有多个解,因此向量是线性相关的。
因此,唯一需要计算的是向量坐标的行列式(因为它是一个 3×3 行列式,所以可以用 Sarrus 规则求解)。该行列式对应于先前方程组的系数:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-046e05ff603822985510c7bdc8b73021_l3.png)
在这种情况下,行列式不为 0,因此向量是线性无关的。
因此,方程组唯一可能的解是所有未知数都为零的平凡解:
![]()
线性相关和独立向量的性质
向量的线性相关性或独立性具有以下特征:
- 两个比例向量是平行的,因此线性相关,因为它们具有相同的方向。
- 同样,如果两个向量方向不同或不成比例,则它们是线性无关的。
- 三个共面向量(位于同一平面内)线性无关。
- 零向量
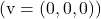
线性依赖于任何向量。
- 一组线性无关的向量生成向量空间并形成向量基。如果三个向量垂直,则它是正交基。如果它的模也等于 1,则这对应于标准正交基。
解决了线性相关性和独立性练习
下面有几个关于线性相关和独立向量的已解决练习可供练习。
练习1
确定以下向量是线性相关还是独立:
![]()
![]()
![]()
我们首先提出线性组合条件:
![]()
![]()
![]()
![]()
前面的等式对应于以下线性方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-58f1b449f48096570437df0ca40f8a8d_l3.png)
一旦我们表述了方程组,我们就可以用它的项来求解矩阵的行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-caa6d4f135e79bb8b6d2368ff7eebefb_l3.png)
在这种情况下,行列式不为0,因此三个向量彼此线性无关。
练习2
将以下向量分类为线性相关或独立:
![]()
![]()
![]()
首先我们提出线性组合的方程:
![]()
![]()
![]()
![]()
根据前面的等式,我们得到以下齐次方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c94610b6f8baef34a1fb4601c148f515_l3.png)
一旦我们表述了方程组,我们就用向量的坐标求解矩阵的行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67678c37fdaf0955ef8bbab8d34379f8_l3.png)
在这种情况下,行列式相当于 0,因此三个向量彼此线性相关。
练习3
对于以下三个向量,指出哪些向量对是线性相关的,哪些对是线性无关的。
![]()
判断一对向量是否线性相关或独立的最简单方法是检查它们是否成比例。
我们首先检查向量
![]()
与向量
![]()
![]()
其次,我们检查向量
![]()
与向量
![]()
![]()
最后,我们测试向量
![]()
与向量
![]()
![]()
因此,唯一一对彼此线性依赖的向量是
![]()
和
![]()
此外,它们的关系如下:
![]()
或同等学历:
![]()
另一方面,其他向量对是线性无关的。
练习4
研究以下 4 个向量彼此之间的线性相关性或独立性:
![]()
![]()
![]()
![]()
我们首先提出线性组合条件:
![]()
![]()
![]()
![]()
在本例中,我们有一个包含 3 个方程组和 4 个未知数的系统:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9451263e5a31994569292e32666d93e_l3.png)
我们无法求解整个系统矩阵的行列式,因为只能确定方阵。因此,我们必须计算 3×3 行列式的所有可能组合,并查看其中一个是否等于 0,在这种情况下,向量将线性相关,另一方面,如果所有行列式都不同于 0,则 4 个向量将是线性独立的。
我们计算系数的行列式
![]()
和
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-488d7848a40aa9a91bd5b3aa1f09b774_l3.png)
前 3 个系数(或前 3 个向量)的行列式不为零。现在我们尝试使用系数的行列式
![]()
和
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1475a77f10ea0c16147a6f9c3f611b4_l3.png)
我们获得了零行列式,因此无需计算其他行列式,因为我们已经知道 4 个向量是线性相关的。
练习5
计算值
![]()
使得以下向量是线性无关的:
![]()
![]()
![]()
首先我们提出线性组合的方程:
![]()
![]()
![]()
![]()
从前面的向量方程,我们得到以下齐次方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l}3a_1-2a_2+a_3= 0 \\[2ex] -a_1+4a_2+3a_3 =0\\[2ex] 5a_1+7a_2+ka_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16f88cbf406c1faf61307b99179a5de6_l3.png)
一旦我们表述了方程组,我们就尝试求解该方程组的行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3&-2&1\\[1.1ex] -1&4&3 \\[1.1ex] 5&7&k \end{vmatrix} =10k-120](https://mathority.org/wp-content/ql-cache/quicklatex.com-d748080bb1cacc1c80a35ef633a2d85e_l3.png)
该陈述告诉我们向量必须是线性相关的。因此行列式必须等于零:
![]()
![]()
![]()
![]()
因此,该常数必须等于 12,以便矢量具有线性相关性。