在这里,您将了解什么是链式法则以及如何使用链式法则导出函数。此外,您将能够看到使用链式法则求解导数的几个示例,甚至可以练习应用链式法则的导数的分步求解练习。
什么是链式法则?
链式法则是用于推导复合函数的公式。链式法则指出复合函数f(g(x))的导数等于导数f'(g(x))乘以导数g'(x) 。
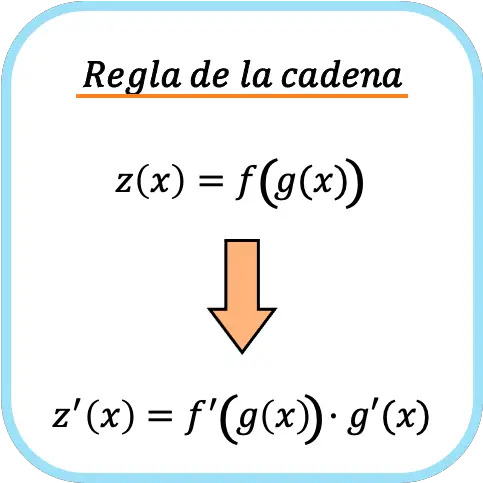
➤参见: 复合函数
非正式地,链式法则通常被认为是对函数进行微分,然后将其乘以函数中的值。
链式法则公式使我们能够更轻松地微分复合函数,因为如果我们要使用导数定义的极限来微分函数的组合,我们将不得不进行大量计算。
另一方面,必须考虑到该规则仅用于求复合函数的导数,而不用于求任何类型的函数或函数运算的导数。例如,一个非常常见的错误是错误地将链式法则应用到功能性产品中,如下所示:
![]()
❌
仅当一个函数包含在另一个函数中时,才能使用链式法则。
![]()
✅
具有链式法则的导数示例
给出了链式法则的定义,我们将以链式法则为例推导出几个函数。请记住,如果在示例中您不明白如何使用链式法则导出函数,您可以在评论中询问我们!
实施例1
在此示例中,我们将使用链式法则导出 x 平方的自然对数:
![]()
自然对数的导数等于其自变量的 1 倍,因此导数
![]()
是:
![]()
![]()
另一方面,x 的 2 次方导数为 2x:
![]()
最后,我们应用链式法则计算整个函数的导数。复合函数的导数将是我们刚刚找到的两个导数的乘积:
![]()
![]()
实施例2
在第二个示例中,我们将基于多项式导出势函数:
![]()
为了导出幂,我们需要将原始指数放在它的前面,并从指数中减去一个单位,因此不应用链式法则的势函数的导数将是:
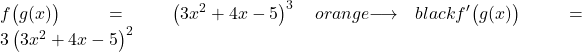
现在我们推导括号里的内容:
![]()
最后,我们使用链式法则来求解整个函数的导数,这将是之前计算的两个导数的乘积:
![]()
![]()
实施例3
在这种情况下,我们将求解 x 的三次方加上 7x 的正弦导数:
![]()
事实上,它是一个函数的复合,因为我们在正弦函数中有函数 x 3 +7x,因此我们可以使用链式法则来求复合函数的导数。
一方面,正弦的导数是余弦,因此外函数的导数将是余弦,其参数与正弦相同:
![]()
另一方面,x 3 +7x 的导数是 3x 2 +7。
![]()
因此,复合函数的导数是两个导数的乘积:
![]()
![]()
用链式法则解决导数练习
练习1
使用链式法则导出以下复合函数:
![]()
外函数是势函数,因此要计算其导数,必须应用以下公式:
![]()
![]()
然后我们计算里面函数的导数。它是幂的减法,因此要计算其导数,您必须将以下公式应用于其每一项:
![]()
![]()
![]()
简而言之,复合函数的导数是找到的两个导数的乘积:
![]()
![]()
练习2
使用链式法则求解以下复合函数的导数:
![]()
首先,我们求外函数的导数:
![Rendered by QuickLaTeX.com \begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e5d21c7196c7ebaeaf6ca11762ca251_l3.png)
现在我们求解内部函数的导数:
![]()
因此整个函数的导数为:
![]()
![]()
练习3
使用链式法则计算以下函数组合的导数:
![]()
它是一个指数函数,因此要计算其导数,必须应用以下公式:
![]()
![]()
我们还将函数与函数的指数区分开来:
![]()
我们使用链式法则求整数复合函数的导数:
![]()
![]()
练习4
使用链式法则求以下复合函数的导数:
![]()
这是函数的组合,因为无理函数的参数中有一个正弦函数和一个线性函数。所以我们首先计算根的导数:
![]()
![Rendered by QuickLaTeX.com f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e909efbe50930f94cce0b2485b060046_l3.png)
现在我们从激进派中得出这个论点。它是函数的和,因此导数将是每一项的导数之和:
![]()
因此整个函数的导数等于两个计算导数的乘积:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fad132b49a5faab86a3955efd5422973_l3.png)
练习5
使用链式法则导出以下函数组合:
![]()
要应用链式法则,您必须求幂和多项式的导数,然后将它们相乘。因此,我们使用相应的公式得出功率:
![]()
![]()
其次,我们从指数导出多项式函数:
![]()
而链式法则告诉我们,整个函数的导数就是我们刚刚找到的导数的乘积:
![]()
![]()
练习6
![]()
显然,这个问题中的函数是复合函数,因为在自然对数的参数中,我们有两种不同类型函数的乘积。所以我们首先对对数求导:
![]()
![]()
其次,我们从对数参数导出函数。这是两个函数的乘法,因此必须使用以下公式进行推导:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-643ddf7ec82cbcc3bc685ceadf59da98_l3.png)
因此,根据链式法则,整个函数的导数将是两个导数的乘积:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6912d0951fb85a61df21cbed282000f2_l3.png)
练习7
使用链式法则求解以下函数的导数:
![]()
这是一个函数的组合,因此我们将对数及其参数分别微分,然后乘以导数。
因此,首先我们对以 9 为底的对数求微分:
![]()
![]()
现在我们计算对数参数的导数。请注意,数字 e 的参数中有一个函数,即它是一个复合函数,因此我们还需要应用链式法则来推导该函数:
![]()
![]()
因此,对数整数参数的导数将是:
![]()
最后,整个函数的导数将是 f'(g(x)) 和 g'(x) 的乘积:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a702df902c9f1eff66e14836a262c0a_l3.png)
练习8
使用链式法则导出以下复合函数:
![]()
在本练习中,我们有多个函数的组合,因此我们必须多次应用链式法则。我们首先从正弦导出三角函数,其导数是余弦:
![]()
现在我们使用链式法则计算正弦参数的导数:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e1c2492990456e277e493c898cb3924_l3.png)
最后,我们再次应用链式法则得到整个函数组合的导数:
![]()
![]()
链式法则证明
最后,我们将证明链式法则公式。为此,我们将从导数的数学定义开始:
![]()
令z为由两个函数组成的函数:
![]()
那么应用该定义的函数z的导数将是:
![]()
如您所知,您可以将分数乘以或除以同一项,因为这不会改变结果。因此,我们可以继续下一步:
![]()
我们重新排列分数的分母:
![]()
通过应用极限的性质,我们可以将上述极限一分为二。由于乘积的极限等于极限的乘积:
![]()
这个表达式等价于以下内容:
![]()
因此,链式法则公式被证明了,因为我们是从导数的定义得出它的。