水平渐近线

在本文中，我们解释什么是函数的水平渐近线以及它们的计算方法。此外，您将找到此类渐近线的几个示例，以充分理解该概念，此外，您将能够通过已解决的水平渐近线练习进行练习。

什么是水平渐近线？

函数的水平渐近线是一条水平线，其图形无限接近该水平线而不会与之相交。因此，水平渐近线的方程为y=k ，其中k是水平渐近线的值。

也就是说，如果x接近无穷大时函数的极限等于k ，则k是水平渐近线。

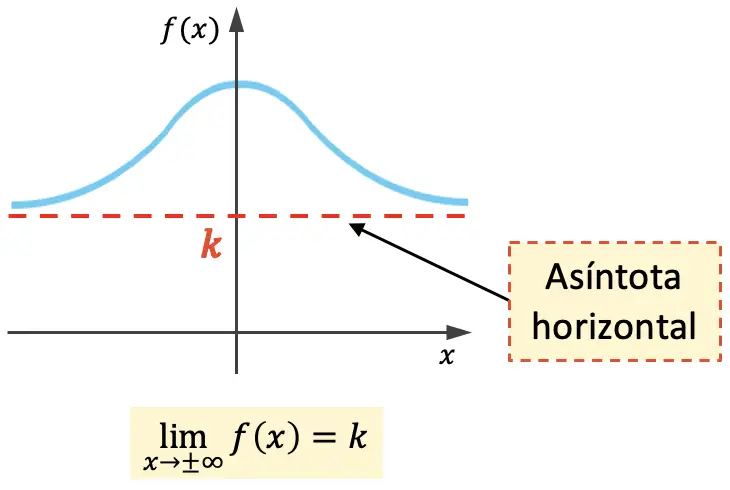
上面的函数在图形的两侧都有水平渐近线，但函数只能在一侧有水平渐近线：

• 如果至少无穷大的极限给出实数，则该函数具有左水平渐近线。
• 如果正无穷大的极限给出实数，则该函数在右侧有一条水平渐近线。

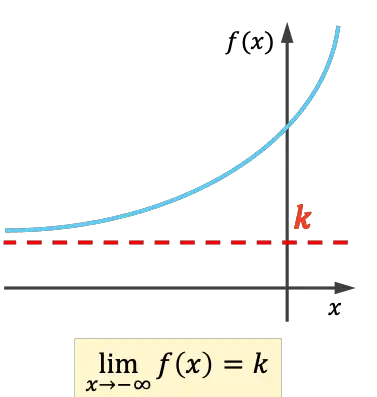
如何计算函数的水平渐近线

要计算函数的水平渐近线，必须遵循以下步骤：

1. 计算函数的无穷大极限（+∞ 和 -∞）。
2. 如果无穷大的极限给出实数 (k)，则直线 y=k 是函数的水平渐近线。
3. 如果两个极限都不对应于实数，则该函数没有水平渐近线。

水平渐近线示例

因此，您可以看到如何完成此操作的示例，我们将从以下有理函数中删除所有水平渐近线：

要确定水平渐近线，需要计算函数在负无穷大和正无穷大处的极限：

➤参见： 如何解决无穷大与无穷大之间的无穷不定性

无穷远处的两个极限为 1，因此y=1 是该函数的唯一水平渐近线。

下面是以图形方式表示的函数。正如您所看到的，该函数非常接近 y=1（在正无穷大和负无穷大处），但它从未触及它，因为它是水平渐近线。

注意：在某些特殊情况下，函数会在一个或多个点与水平渐近线相交，但一般来说，函数的图形永远不会与其渐近线相交。

另一方面，该函数在 x=1 处也有垂直渐近线。因为，正如您从图中看到的那样，它非常接近 x=1 线，但从未达到该值。

解决了水平渐近线的问题

练习1

求以下分数函数的水平渐近线（如果有）：

为了确定有理函数的水平渐近线，需要计算函数无穷远处的极限：

在这种情况下，不定形式 ∞/∞ 的结果是最高次 x 的系数相除，因为分子和分母具有相同的阶数。

函数的正无穷大和负无穷大处的极限为 2，因此y=2 是水平渐近线，并且是该函数具有的唯一渐近线。

练习2

求以下有根有理函数的所有水平渐近线：

为了找到函数的水平渐近线，我们首先计算正无穷大的极限：

然后我们求解函数的负无穷极限：

➤ 如果您对如何解决无穷大的极限有任何疑问，我们建议您查看上面的链接，了解如何解决无穷大之间的无限不确定性。

在这种情况下，我们获得了两个不同的无穷远极限值。因此，该函数有两个水平渐近线：y=3 是右侧函数的水平渐近线，另一方面，y=-3 是左侧函数的水平渐近线。

练习3

计算以下分段定义函数的水平渐近线：

要计算函数的水平渐近线，没有公式，但必须计算正负无穷大的极限。

因此，为了找到至少无限的极限，我们采用第一部分中定义的函数：

因此，线 y=0 是函数左侧的水平渐近线。

现在我们通过使用第二部分中定义的函数来计算正无穷大的极限：

因此，线 y=1/2 是函数右侧的水平渐近线。