正则矩阵 - Mathority

在此页面上，您将看到什么是正规矩阵以及正规矩阵的示例。此外，您还会发现此类矩阵的性质以及逐步解决的练习。

什么是正规矩阵？

正常的数组定义是：

普通矩阵是一个复矩阵，乘以它的共轭转置矩阵等于共轭转置矩阵与其本身的乘积。

$A\cdot A^*=A^*\cdot A$

金子

$A^*$

是共轭转置矩阵

$A$

。

然而，如果它们是实数矩阵，则前面的条件相当于说矩阵与其转置可交换，也就是说：

$A\cdot A^t=A^t\cdot A$

因为，显然，实数矩阵的共轭转置矩阵就是简单的转置（或转置）矩阵。

正规矩阵的示例

复数示例

以下维度为 2×2 的复方矩阵是正规矩阵：

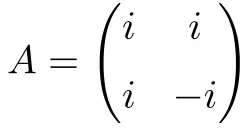
其正常性演示如下：

$\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

实数示例

下面的 2 阶实数方阵也是正规的：

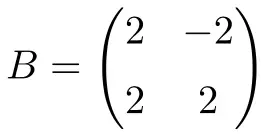
在这种情况下，由于它只有实数，为了证明它是正常的，只需验证矩阵与其转置可交换：

$\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

正规矩阵的性质

正规矩阵具有以下特征：

所有正规矩阵都是可对角化矩阵。

每个酉矩阵也是一个正规矩阵。

同样，埃尔米特矩阵是一个正规矩阵。

同样，反埃尔米特矩阵也是一个正规矩阵。

如果A是正规矩阵，则共轭转置矩阵A*的特征值（或多个特征值）就是A的共轭特征值。

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i$

在正规矩阵中，不同特征值相关的特征向量（或特征向量）是正交的。

如果一个矩阵仅由实数组成并且是对称的，那么它同时也是一个正规矩阵。

同样，反对称实矩阵也是正规矩阵。

最后，任何由实数组成的正交矩阵也是正规矩阵。

解决了正规矩阵的练习

练习1

验证以下维度为 2 × 2 的复数矩阵是否为正规矩阵：

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

查看解决方案

为了证明矩阵是正规的我们必须首先计算它的共轭转置：

$\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

现在我们通过在两个可能的方向上将矩阵 A 乘以矩阵 A* 来进行验证：

$\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

两次乘法的结果相同，因此矩阵 A 是正规矩阵。

练习2

证明以下大小为 2 × 2 的实矩阵是正规矩阵：

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

查看解决方案

由于在这种情况下我们处理的是只有实数的环境，因此只要验证矩阵 A 及其转置之间的矩阵乘积无论乘法方向如何都给出相同的结果就足够了：

$\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

两个乘积的结果相同，因此矩阵 A 是正规的。

练习3

确定以下 2 阶复数矩阵是否为正规矩阵：

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

查看解决方案

为了检查矩阵是否正常，我们必须首先计算它的共轭转置：

$\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

现在我们检查矩阵 A 及其共轭转置是否可切换：

$\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

两次乘法的结果相同，因此矩阵 A 是正规矩阵。

练习4

验证以下维度为 3×3 的实矩阵是否为正规矩阵：

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

查看解决方案

该矩阵完全由实数元素组成，足以验证矩阵 A 及其转置之间的矩阵乘积与乘法的方向无关：

$\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

两个乘积的结果相同，因此矩阵 A 是正规的。

练习5

判断以下 3×3 阶复矩阵是否为正规矩阵：

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

查看解决方案

首先，我们计算矩阵的共轭转置：

$\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

现在我们需要在两个可能的方向上进行矩阵 A 与其共轭转置之间的矩阵乘法。然而，A 的共轭转置矩阵等于矩阵 A 本身，因此它是 Hermitian 矩阵。因此，从正规矩阵的性质可知 A 是正规矩阵，因为每个 Hermitian 矩阵都是正规矩阵。

什么是正规矩阵？

正规矩阵的示例

复数示例

实数示例

正规矩阵的性质

解决了正规矩阵的练习

练习1

练习2

练习3

练习4

练习5

发表评论 取消回复

发表评论取消回复