正比例函数

在本文中，我们解释什么是正比例函数、它们的公式是什么、如何在图形中表示它们，以及如何从给定点计算它们的方程。

什么是正比例函数？

正比例函数也称为线性函数。

请记住，如果一个数量的价值增加而另一个数量也增加，则两个数量成正比，反之亦然。

正比例函数的公式

定义正比例函数的公式如下：

其中 y 是自变量，x 是因变量，ym 是函数的斜率或比例常数。

正如您所看到的，使用这个公式很容易计算 y 的大小值，只需将 x 的大小值乘以函数的斜率（每个正比例函数的特征）即可。

例如，如果我们有以下正比例函数：

如果我们想确定 x 为 5 时 y 的大小，只需将函数 (3) 的斜率乘以 5：

正比例函数的图形表示

接下来，我们将了解如何绘制正比例函数的图表。我们将做以下练习作为示例：

要在图形上表示正比例函数，只需绘制一条穿过坐标原点（点 (0,0)）并具有函数斜率的线。

在这种情况下，我们想要表示的函数的斜率为

因此，对于 x 的每一个单位，直线必须增长 y 的两个单位。

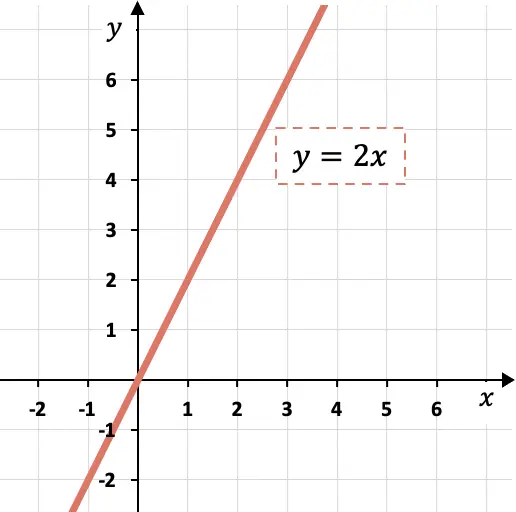
从图中可以看出，如果斜率等于 2，则意味着 y 幅度增加是 x 幅度的两倍。

正比例函数与仿射函数具有非常相似的图形，但它们是两种不同类型的函数。您可以在以下链接中了解仿射函数和线性函数之间的区别：

➤参见：线性函数和仿射函数的区别

如何求正比例函数

如果我们知道正比例函数的一点，我们就可以很容易地找到它的方程。让我们看看如何通过解决正比例函数问题来实现这一点：

• 画家绘制的房间数量大约与他工作的时间成正比，也就是说，他工作的时间越多，他可以绘制的房间就越多。如果我们知道他在一天 8 小时内粉刷了两个完整的房间，那么将粉刷的房间数量与工作时间联系起来的正比函数是什么？

首先，我们需要确定哪个是因变量，哪个是自变量。绘制的作品数量取决于工作时间，而不是相反。因此，自变量 (x) 是工作小时数，因变量 (y) 是粉刷房间的数量。

问题告诉我们，画家可以在8小时内粉刷2个房间，因此函数的图形必须经过点(8,2)。

此外，该陈述表明这两个量具有正比例关系，这意味着它们在数学上与正比例函数公式相关：

现在我们可以通过将点 (8,2) 的坐标代入方程来计算函数的斜率值：

最后，我们求解方程的未知 m：

简而言之，问题的正比例函数为：

你可能还喜欢：

• 反比例函数
• 常数函数