在本文中,我们将了解如何找到曲线的切线方程。此外,您还可以通过不同难度级别的已解决练习进行训练。
函数在一点的切线方程
函数 f(x) 在 x=x 0处的切线方程为:
![]()
其中点P(x 0 ,y 0 )是切线与函数重合的点。而切线的斜率m等于曲线在x 0点处的导数,即m=f'(x 0 )。

在上图中你可以看到一条曲线
![]()
用与函数相切的蓝色线和橙色线表示
![]()
关于
![]()
,因为它们只有这一点的共同点。那么,这条切线的方程是
![]()
,其斜率为
![]()
。
如何求正切方程
要找到函数在一点的切线方程,您需要执行以下操作:
- 通过计算函数在切点处的导数来求出切线的斜率。
- 确定切线上的一点。
- 使用计算出的斜率和切线点求出切线方程。
曲线切线方程示例
了解了正切方程的理论后,让我们看看如何通过逐步求解示例来计算正切方程:
- 计算曲线的切线方程
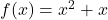
关于
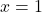
。
我们知道,正切方程总是以下形式:
![]()
首先要做的是计算直线的斜率。因此,切线的斜率,
![]()
,将是曲线在切点 x=1 处的导数值,即
![]()
因此,我们对函数进行微分,然后计算
![]()
![]()
![]()
![]()
一旦我们知道了
![]()
,我们需要找到一个点
![]()
的切线来完成切线方程。
切线方程和曲线方程总是有一个公共点,在本例中是
![]()
。因此,就像曲线
![]()
通过这个点,我们可以通过计算找到该点的另一个分量
![]()
![]()
![]()
因此切点为:
![]()
曲线和切线都经过该点,所以我们也可以用它来求切线的方程。
剩下的就是将找到的斜率和切线点的值代入其方程:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0321e19825c08a1f47a00b2cf625088f_l3.png)
简而言之,正切方程为:
![]()
您还可以用直线的显式方程来表达切线的方程:
![]()
下面你可以看到代表的曲线
![]()
和它的切线
![]()
![]()
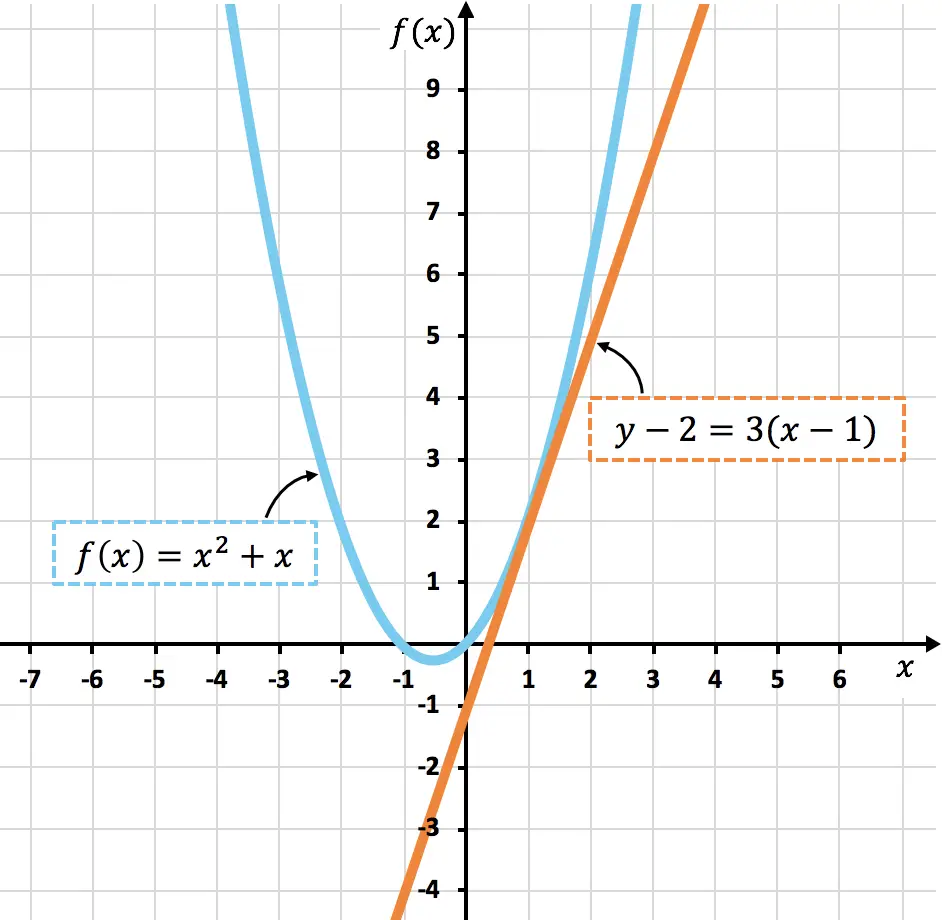
正如你所看到的,曲线
![]()
和切线
![]()
他们只有一个共同点
![]()
,正如我们计算的那样。
已解答的正切方程练习
练习1
计算曲线的切线方程
![]()
关于
![]()
正切方程始终采用以下形式:
![]()
步骤一:计算切线的斜率
斜率m是曲线在切点处的导数值。因此,在这种情况下
![]()
![]()
![]()
![]()
第二步:找到切线上的点
切线方程和曲线方程总是有一个公共点,在本例中为
![]()
。因此,就像曲线
![]()
通过这个点,我们可以通过计算找到该点的另一个分量
![]()
![]()
![]()
因此,曲线和切线都经过的点就是该点
![]()
第三步:写出正切方程
剩下的就是将找到的斜率和切线点的值代入其方程:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1622c6ecd4d43bb4fc4901b437464652_l3.png)
因此,正切方程为:
![]()
练习2
计算曲线的切线方程
![]()
在坐标原点。
坐标原点指的是该点
![]()
因此,我们必须计算函数在该点的正切值
![]()
首先,我们通过计算坐标原点处的导数来确定切线的斜率值:
![]()
![]()
![]()
在这种情况下,我们已经知道切线经过的点。因为该语句告诉我们直线必须在坐标原点处与曲线相切,也就是说在该点
![]()
所以曲线和切线共有的点就是点
![]()
最后,只需将找到的斜率和切线点的值代入方程即可:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)](https://mathority.org/wp-content/ql-cache/quicklatex.com-de8e4e9dbb7a5bca1d591612abcf7730_l3.png)
综上,正切方程为:
![]()
![]()
练习3
计算曲线的切线
![]()
与右边平行
![]()
。
在这个问题中,我们被告知切线必须平行于直线
![]()
如果两条线具有相同的斜率,则它们是平行的。因此,切线必须具有与直线相同的斜率
![]()
这意味着我们需要找到直线的斜率
![]()
为此,我们清除变量并:
![]()
所以直线的斜率
![]()
是 4,因为当 y 明确时,直线的斜率是 x 的乘积。
因此,切线的斜率也必须为 4,因为要使它们平行,它们必须具有相同的斜率。
![]()
在这种情况下,它们不会告诉我们曲线和切线之间的切点。但我们知道曲线在切点处的导数等于切线的斜率,即
![]()
。那么我们如何知道的价值
![]()
,我们可以从方程中找到 x 0
![]()
为此,我们首先计算
![]()
![]()
现在我们解决
![]()
知道
![]()
![]()
![]()
![]()
![]()
![]()
![]()
一旦我们知道了该点的x坐标,我们就可以通过计算找到该点的另一个坐标
![]()
![]()
因此,曲线和切线都经过的点就是该点
![]()
剩下的就是将找到的斜率和切线点的值代入其方程:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f1f49e9bef505c5c71cffd15f0d29d0_l3.png)
正切方程为:
![]()
练习4
计算曲线的切线
![]()
与 X 轴形成 45° 角。
问题陈述告诉我们切线必须与 X 轴形成 45° 角。在这些情况下,必须应用以下公式来计算斜率值:
![]()
![]()
该语句没有指定曲线和切线之间的切点。但我们知道,曲线在切点处的导数就相当于切线的斜率,即
![]()
。因此,我们可以通过求解方程来计算 x 0
![]()
为此,我们首先计算
![]()
![]()
现在我们解决
![]()
知道
![]()
![]()
![]()
![]()
![]()
![]()
![]()
一旦我们知道了该点的x坐标,我们就可以通过计算找到该点的另一个坐标
![]()
![]()
因此,曲线和切线都经过的点就是该点
![]()
剩下的就是将找到的斜率和切线点的值代入其方程:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=1 \qquad P(-1,-2) \end{array} \right\} \longrightarrow \ y -(-2)= 1(x-(-1))](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ed772b3993de50c4c67631a6fd33040_l3.png)
最后,我们进行运算来求正切方程:
![]()
![]()
![]()