正交矩阵 - Mathority

在此页面上，您将看到什么是正交矩阵以及它们与矩阵的逆矩阵的关系。您还将看到几个示例来完全理解它。此外，我们还教您检查任何正交矩阵的公式，通过该公式您将知道如何快速找到一个正交矩阵。最后，您将找到这些特定矩阵的属性和应用以及典型的已解决考试练习。

什么是正交矩阵？

正交矩阵的定义如下：

正交矩阵是一个实数方阵，乘以它的转置（或转置）等于单位矩阵。即满足以下条件：

$A\cdot A^t = A^t \cdot A =I$

金子

$A$

是一个正交矩阵并且

$A^t$

表示其转置矩阵。

为了满足这个条件，正交矩阵的列和行必须是正交单位向量，即它们必须形成正交基。因此，一些数学家也将它们称为正交矩阵。

正交矩阵的逆

另一种解释正交矩阵概念的方法是通过逆矩阵，因为正交矩阵的转置（或转置）矩阵等于其逆矩阵。

要充分理解该定理，了解如何反转矩阵非常重要。在此链接中，您将找到矩阵的逆矩阵及其所有属性的详细说明，甚至还有逐步解决的练习可供练习。

使用正交矩阵条件和逆矩阵的主要属性，可以轻松地证明正交矩阵的逆矩阵与其转置等效：

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

因此，正交矩阵将始终是可逆矩阵，或者换句话说，它将是正则或非简并矩阵。

接下来，我们将通过几个正交矩阵的例子来完成对一切概念的理解。

2×2 正交矩阵示例

下面的矩阵是一个维度为2×2的正交矩阵：

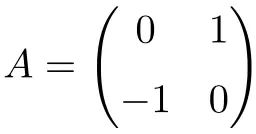
我们可以通过转置计算乘积来检查它是否正交：

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

由于结果给出了相同的矩阵，我们验证 A 是正交矩阵。

3×3 正交矩阵示例

下面的矩阵是一个维度为3×3的正交矩阵：

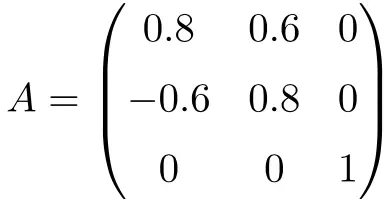
我们可以通过将矩阵 A 乘以其转置来证明它是正交的：

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

由于解是酉矩阵，因此我们证明 A 是正交矩阵。

求 2×2 正交矩阵的公式

然后我们将看到所有 2 阶正交矩阵都遵循相同模式的证明。

考虑大小为 2×2 的通用矩阵：

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

为了使该矩阵正交，必须满足以下矩阵方程：

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

求解矩阵乘法，我们得到以下方程：

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

如果仔细观察，这些等式看起来很像基本的毕达哥拉斯三角关系：

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

因此，得到满足式(1)和式(3)的项为：

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

另外，将这些值代入第二个方程，我们得到两个角度之间的关系：

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

即必须满足以下两个条件之一：

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

因此，总而言之，正交矩阵必须具有以下两个矩阵之一的结构：

金子

$\theta$

是一个实数。

事实上，如果作为一个例子我们授予价值

$\displaystyle\theta=\frac{\pi}{2}$

采用第一种结构，我们将得到在“2×2正交矩阵示例”一节中验证为正交的矩阵：

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

正交矩阵属性

此类矩阵的特点是：

正交矩阵永远不可能是奇异矩阵，因为它总是可以逆的。从这个意义上说，正交矩阵的逆是另一个正交矩阵。

任何正交矩阵都可以对角化。然后我们说正交矩阵是可正交对角化的。

正交矩阵的所有特征值或特征值的模数都等于 1。

任何仅由实数组成的正交矩阵也是正规矩阵。

复数环境中正交矩阵的类似物是酉矩阵。

显然，单位矩阵是一个正交矩阵。

维度为 n × n 的正交矩阵的集合以及矩阵乘积的运算形成一个称为正交群的群。也就是说，两个正交矩阵的乘积等于另一个正交矩阵。

此外，正交矩阵与其转置相乘的结果可以用 Kronecker delta 表示：

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

最后，正交矩阵的行列式总是+1或-1。

$\displaystyle \text{det}(A)=\pm 1$

正交矩阵的求解练习

然后我们将解决正交矩阵的练习。

给定以下 3 阶方阵，找到的值
$a$

和

$b$

使其正交：

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

为了满足矩阵的正交性，矩阵与其转置的乘积必须等于单位矩阵。所以：

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

我们将矩阵相乘：

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$