横向限制

在本文中，我们将解释什么是函数的横向极限（并附有示例）。我们还教您如何以图形和数字方式计算函数的左侧和右侧极限。此外，您将能够通过逐步解决横向限制的练习进行训练。

横向限制是多少？

函数在某一点的横向极限研究函数在该点周围的行为。有左侧极限和右侧极限，分别分析函数在考虑点左侧和右侧的值。

左右侧向限制

正如我们在横向边界的定义中看到的，有两种类型：左侧边界和右侧边界。

函数的左极限在分析极限的点处用减号表示，而右极限则用加号表示。

看下面的例子可以更好地理解横向限制的含义：

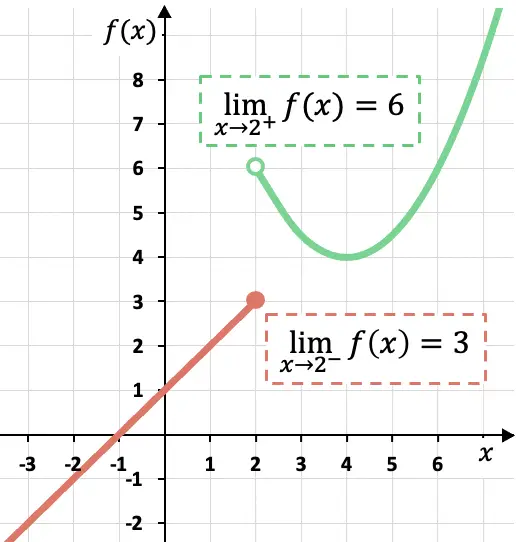
正如您在此分段函数的图形表示中所看到的，横向限制取决于计算它们的一侧。

在这种情况下，当 x 从左边接近 2 时，函数会接近 3，因为当x从左边接近 x=2 时，函数会取更接近 3 的值。

另一方面，函数在 x=2 处的直线的横向极限值为 6。因为如果我们通过直线接近点 x=2，函数的值会越来越接近 f(x)= 6.

另一方面，您应该知道横向限制与普通限制具有相同的属性。在以下链接中，您可以看到边界属性是什么：

➤请参阅：边界属性

等横向限制

我们刚刚看到了一个函数的边限不同的例子，但是……如果边限相同会发生什么？

如果函数在一点处的两个横向极限都存在并且相等，则函数在该点存在极限，极限的结果就是横向极限的值。

换句话说，要使函数在一点处存在极限，必须满足以下条件：

因此，如果函数在一点处的横向极限不同，则该函数在该点的极限不存在。

另外，函数在点处的极限的存在是函数在点处连续的必要条件。

让我们通过一个例子来完成对横向极限概念的理解：

图形表示的函数点 x=-2 处的横向极限是重合的，因为无论我们从左侧还是从右侧接近 x=-2，函数的值都趋向于 3。因此，函数在 x=-2 处的极限等于 3。

另一方面，在点 x=4 处，横向极限不同，因为从左侧函数接近 f(x)=3，但从右侧函数接近 f(x)=2。因此此时函数的极限不存在。

横向限制的计算

给定横向极限的定义，我们将通过求解以下示例来了解如何以数值方式计算它们：

如果我们照常计算极限，我们就得到实数除以 0 的不确定性：

然而，在计算横向极限时，我们没有得到任何不确定性。

要计算函数在 x=2 处从左侧开始的横向极限，必须取一个小于 x=2 但非常接近的数字，例如 x=1.999。

在这种情况下，分母将是一个非常小的负数，但甚至不是零，通常用零和前面的减号表示：

因此，横向极限的结果是负无穷大，因为任何数字除以 0 都会得到无穷大，正数除以负数都会得到负数：

我们可以通过计算左侧接近 x=2 的值的函数图像来验证该函数是否接近负无穷大。

同样，要找到函数在右侧点 x=2 处的极限，我们可以应用相同的推理：我们取一个大于 2 但非常接近的值，例如 2001。

同理，我们可以通过计算从右边开始越来越接近x=2的函数图像来验证函数是否趋于无穷大。

在下图中，您可以看到所分析的函数。可以看到，函数在左边点x=2处的横向极限是负无穷大，函数在右边点x=2处的横向极限是正无穷大。

横向边界问题已修复

练习1

求以下分段定义函数在定义发生变化的点（x=-2 和 x=4）处的横向极限。

横向极限在 x=-2 点处不重合，左侧函数趋于 f(x)=5，另一方面，右侧函数为常数且值为 3。

当 x 接近 4 时，边限也不同。分段函数从左侧接近 3，但从右侧接近 -2。

练习2

判断下列分段函数的 x 接近 3 时极限是否存在，如果存在，其值是多少。

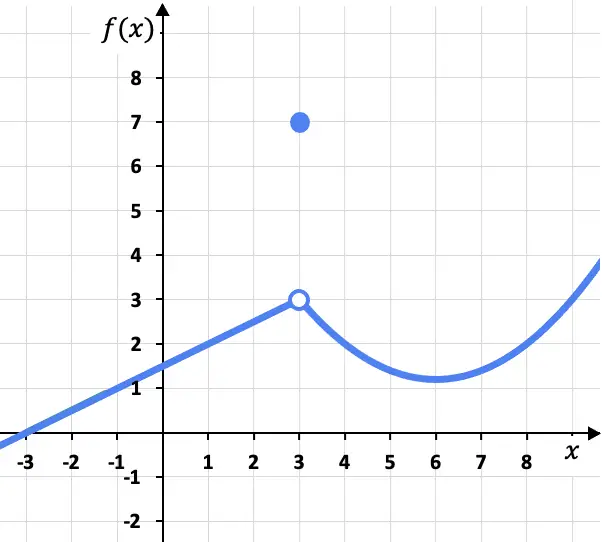
在这个问题中，从左到右的点 x=3 处的横向极限是相同的，因为无论从左还是从右接近，函数都趋向于相同的值 (f(x)=3) 。他的右侧：

因此，根据极限的数学定义，当x趋向于3时函数的极限等于3，因为同一点的两个横向极限在该值处重合：

虽然x=3处函数的极限是3，但必须考虑到此时的函数不是3，而是f(3)=7。正如我们稍后将看到的，这意味着该函数在 x=3 处不连续，而是具有可避免的不连续性。

练习3

计算以下有理函数在点 x=4 处的横向极限。

为了计算 x 从左边趋向于 4 时的极限，我们取一个小于 4 但非常接近它的值，例如 3,999：

因此，当 x 从左侧接近 4 时，横向极限是正无穷大。

为了解决 x 从右侧趋向于 4 时的极限，我们以大于 4 但非常接近 4 的值来计算函数，例如 4,001：

因此，当 x 从右侧接近 4 时，横向极限为负无穷大。

练习4

求在点 x=2 处定义的以下分段函数的极限（如果存在）：